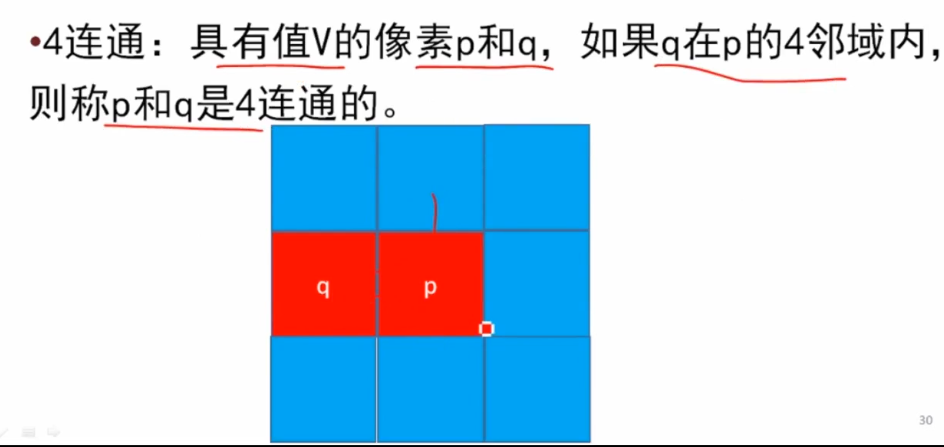
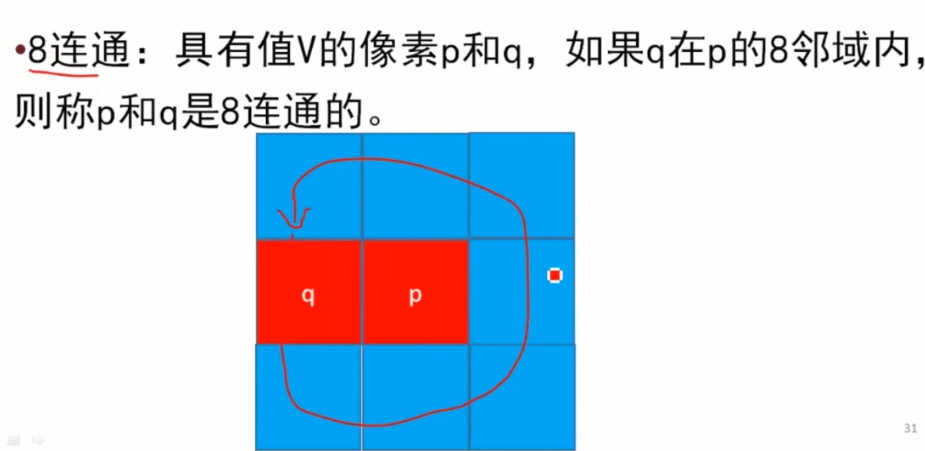
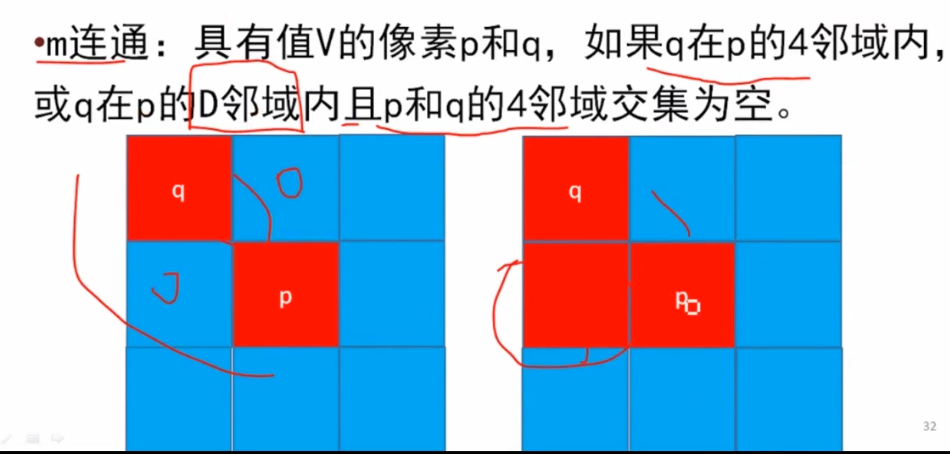
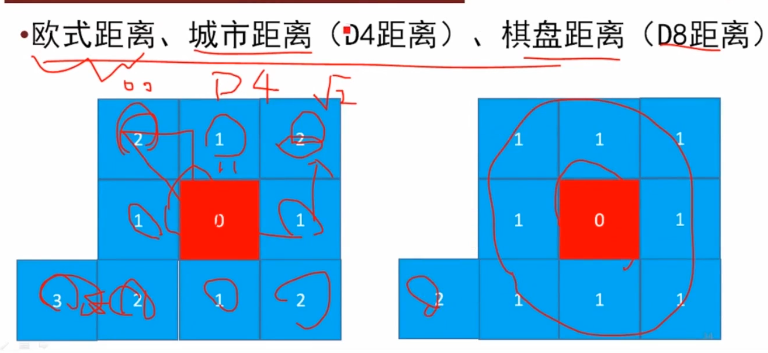
1.问题:什么叫连续？什么叫连续映射，研究拓扑为什么需要连续映射？
每门学科都建立在一些基础概念上，而拓扑学中贯穿着一个概念，就是连续性的概念。
要说明连续的概念，要从函数连续的概念类比。
基础拓扑学笔记(2)--拓扑不变量
基础拓扑学笔记(1)--欧拉定理
CNN FCN U-Net 卷积神经网络学习（1）
前馈神经网络
图像的表示和数字长方体
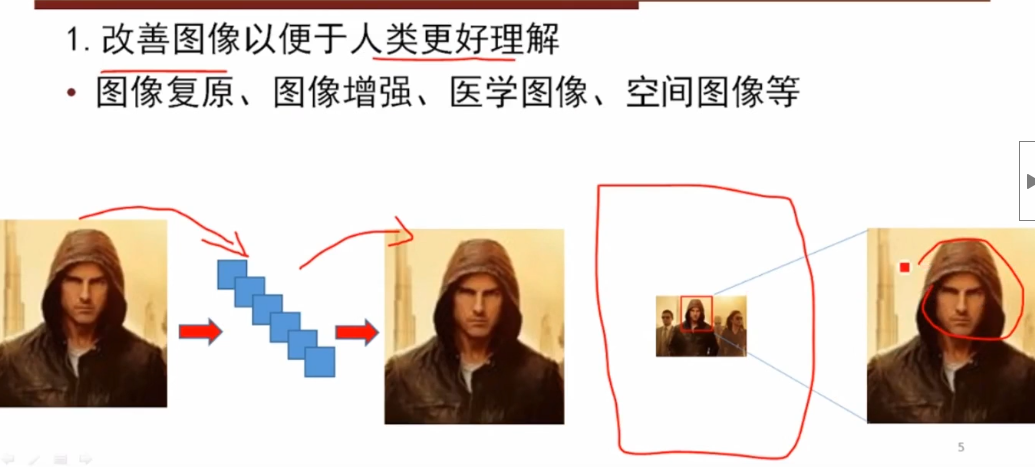
图像在计算机中是一堆按顺序排列的数字,数值为0到255,0表示最暗, 255表示最亮。你可以把这堆数字用一个长长的向量来表示。然而这样会失去平面结构的信息,为保留该结构信息,通常选择矩阵的表示方式: 28x28的矩阵。
上图是只有黑白颜色的灰度图,而更普遍的图片表达方式是RGB颜色模型,即红(Red)、绿(Green) 、蓝(Blue)三原色的色光以不同的比例相加,以产生多种多样的色光。
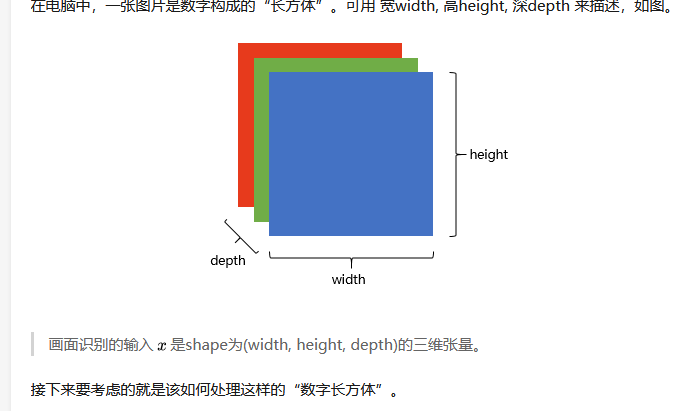
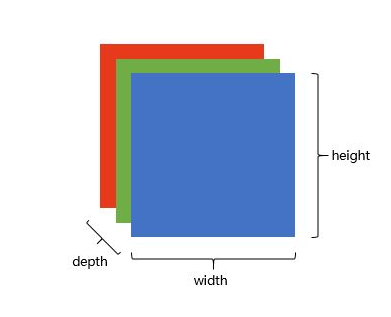
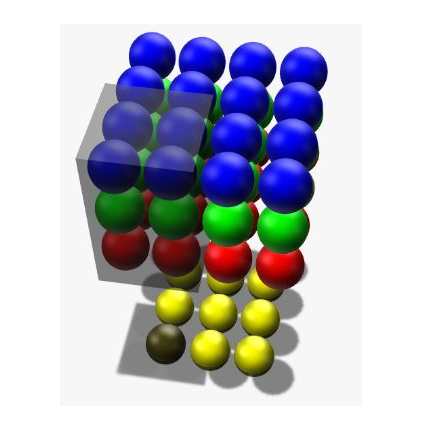
在电脑中,一张图片是数字构成的”长方体” 。可用宽width,高height,深depth来描述,如图。
画面不变性
在决定如何处理”数字长方体”之前,需要清楚所建立的网络拥有什么样的特点。我们知道一个物体不管在画面左侧还是右侧,都会被识别为同一物体,这一特点就是不变性(invariance) ,如下图所示。
我们希望所建立的网络可以尽可能的满足这些不变性特点。为了理解卷积神经网络对这些不变性特点的贡献,我们将用不具备这些不变性特点的前馈神经网络来进行比较。
前馈神经网络的图像识别
方便起见,我们用depth只有1的灰度图来举例。想要完成的任务是:在宽长为4x4的图片中识别是否有下图所示的”横折”。图中,黄色圆点表示值为0的像素,深色圆点表示值为1的像素。我们知道不管这个横折在图片中的什么位置,都会被认为是相同的横折。
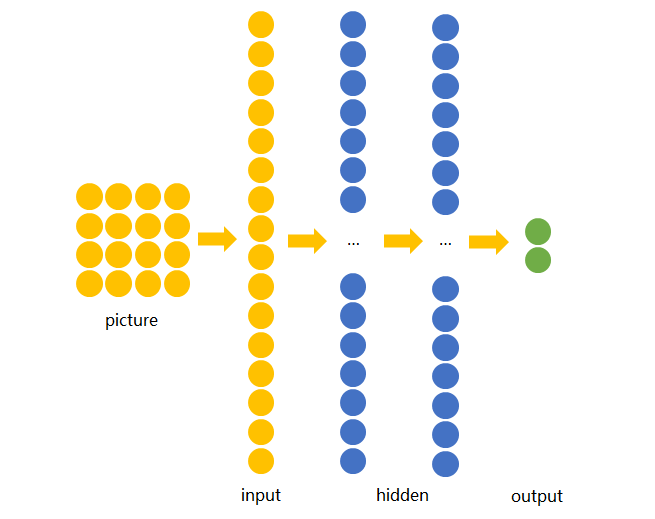
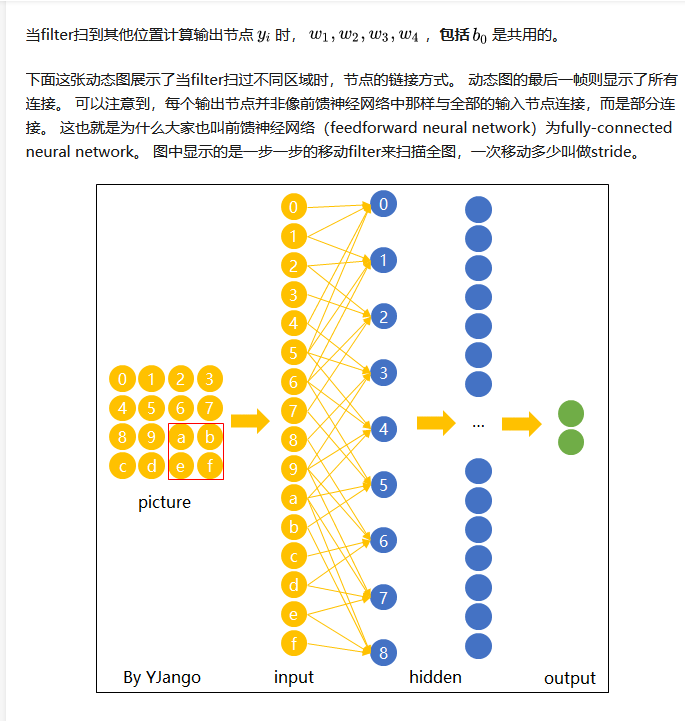
若训练前馈神经网络来完成该任务,那么表达图像的三维张量将会被摊平成一个向量,作为网络的输入,即(width, height, depth)为(4, 4, 1)的图片会被展成维度为16的向量作为网络的输入层。再经过几层不同节点个数的隐藏层,最终输出两个节点,分别表示“有横折的概率”和”没有横折的概率” ,如下图所示。
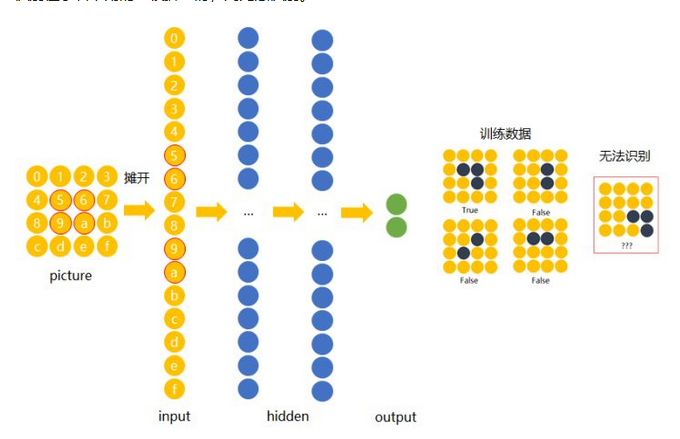
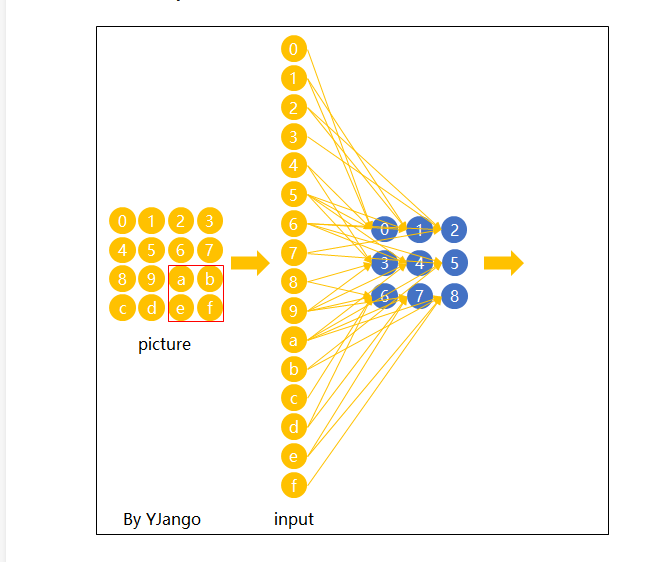
下面我们用数字(16进制)对图片中的每一个像素点(pixel)进行编号。当使用右侧那种物体位于中间的训练数据来训练网络时,网络就只会对编号为5,6,9,a的节点的权重进行调节。若让该网络识别位于右下角的”横折”时,则无法识别。
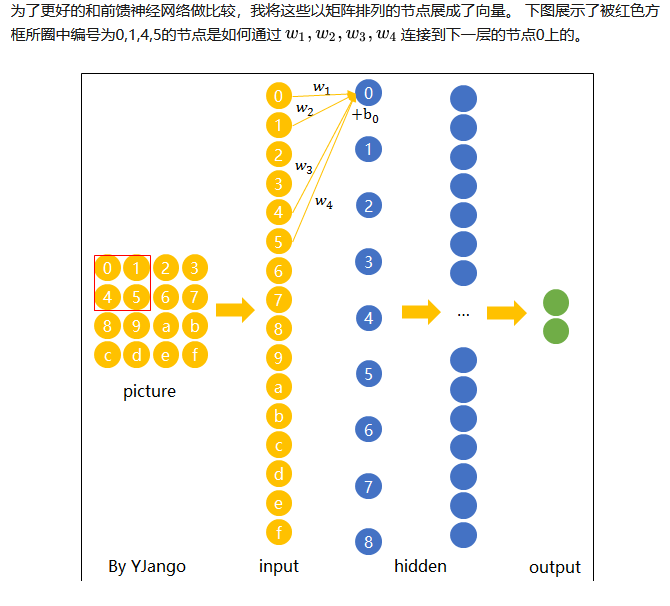
解决办法是用大量物体位于不同位置的数据训练,同时增加网络的隐藏层个数从而扩大网络学习这些变体的能力。
前馈神经网络的缺点
然而这样做十分不效率,因为我们知道在左侧的“横折”也好,还是在右侧的”横折”也罢,大家都是”横折”。为什么相同的东西在位置变了之后要重新学习?有没有什么方法可以将中间所学到的规律也运用在其他的位置?换句话说,也就是让不同位置用相同的权重。
卷积神经网络CNN就是让权重在不同位置共享的神经网络。
CNN的局部扫描
在卷积神经网络中,我们先选择一个局部区域,用这个局部区域去扫描整张图片。局部区域所圈起来的所有节点会被连接到下一层的一个节点上。
CNN的输出
深度为复数的情况
现在我们已经知道了depth维度只有1的灰度图是如何处理的。但前文提过,图片的普遍表达方式是下图这样有3个channels的RGB颜色模型。当depth为复数的时候,每个feature detector是如何卷积的?
在输入depth为1时:被filter size为2x2所圈中的4个输入节点连接到1个输出节点上。
在输入depth为3时:被filter size为2x2,但是贯串3个channels后,所圈中的12个输入节点连接到1个输出节点上。
在输入depth为n时: 2x2xn个输入节点连接到1个输出节点上。
CNN（卷积神经网络）
Facebook 将神经网络用于自动标注算法、谷歌将它用于图片搜索、亚马逊将它用于商品推荐、Pinterest 将它用于个性化主页推送、Instagram 将它用于搜索架构。
然而，应用神经网络网络最经典最流行的案例是进行图像处理。在图像处理任务中，使用卷积神经网络进行图像分类。
图像分类是对输入图像的操作，最终输出一组最好地描述了图像内容的分类（如猫、狗等）或分类的概率。对人类来说，识别是打出生便开始学习的技能之一，对成人来说更是信手拈来，毫不费力。我们只需一眼便能快速识别我们所处的环境以及环绕在我们身边的物体。当我们看到一张图片或是环看四周的时候，无需刻意观察，多数时候也能立即描述出场景特征并标记出每一个对象。快速识别不同模式、根据早前知识进行归纳、以及适应不同的图像环境一直都是人类的专属技能，机器尚未享有。
当计算机看到一张图像（输入一张图像）时，它看的是一大堆像素值。根据图片的分辨率和尺寸，它将看到一个 32 x 32 x 3 的数组（3 指代的是 RGB 值）。假设我们有一张 JPG 格式的 480 x 480 大小的彩色图片，那么它对应的数组就有 480 x 480 x 3 个元素。其中每个数字的值从 0 到 255 不等，其描述了对应那一点的像素灰度。当我们人类对图像进行分类时，这些数字毫无用处，可它们却是计算机可获得的唯一输入。其中的思想是：当你提供给计算机这一数组后，它将输出描述该图像属于某一特定分类的概率的数字（比如：80% 是猫、15% 是狗、5% 是鸟）。
我们想要计算机能够区分开所有提供给它的图片，以及搞清楚猫猫狗狗各自的特有特征。这也是我们人类的大脑中不自觉进行着的过程。当我们看到一幅狗的图片时，如果有诸如爪子或四条腿之类的明显特征，我们便能将它归类为狗。同样地，计算机也可以通过寻找诸如边缘和曲线之类的低级特点来分类图片，继而通过一系列卷积层级建构出更为抽象的概念。这是 CNN（卷积神经网络）工作方式的大体概述，
挑一张图像，让它历经一系列卷积层、非线性层、池化（下采样（downsampling））层和完全连接层，最终得到输出。输出可以是最好地描述了图像内容的一个单独分类或一组分类的概率。
卷积层
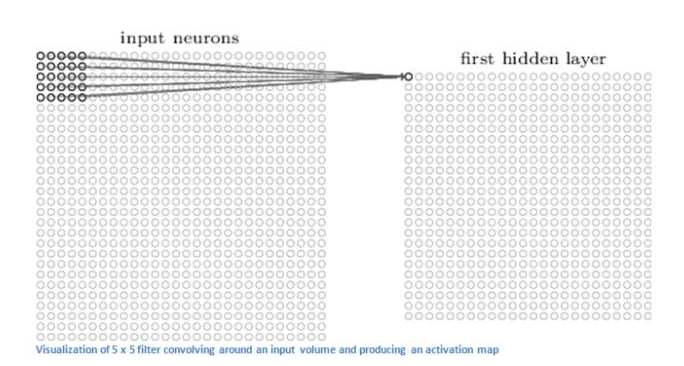
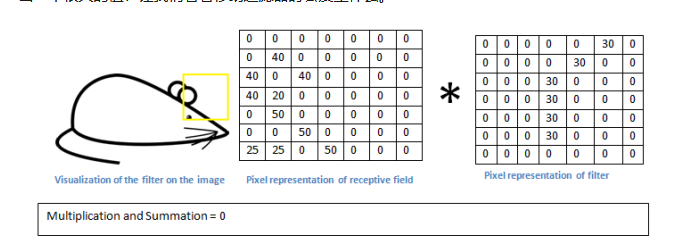
CNN 的第一层通常是卷积层（Convolutional Layer）。首先需要了解卷积层的输入内容是什么。输入内容为一个 32 x 32 x 3 的像素值数组。现在，解释卷积层的最佳方法是想象有一束手电筒光正从图像的左上角照过。假设手电筒光可以覆盖 5 x 5 的区域，想象一下手电筒光照过输入图像的所有区域。
在机器学习术语中，这束手电筒被叫做过滤器（filter，有时候也被称为神经元（neuron）或核（kernel）），被照过的区域被称为感受野（receptive field）。过滤器同样也是一个数组（其中的数字被称作权重或参数）。重点在于过滤器的深度必须与输入内容的深度相同（这样才能确保可以进行数学运算），因此过滤器大小为 5 x 5 x 3。
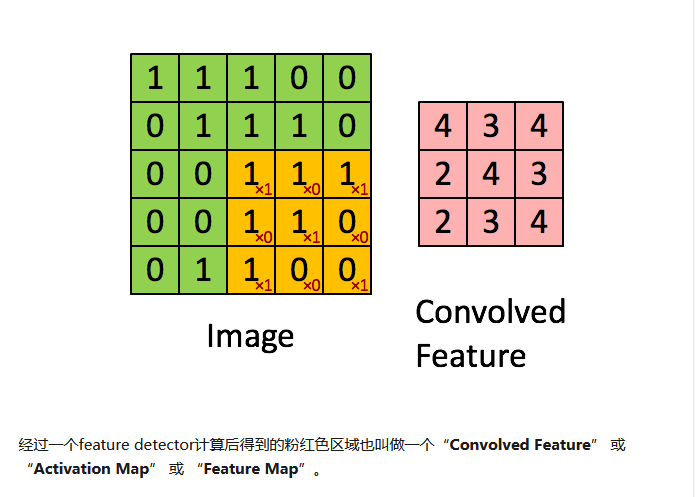
现在，以过滤器所处在的第一个位置为例，即图像的左上角。当筛选值在图像上滑动（卷积运算）时，过滤器中的值会与图像中的原始像素值相乘（又称为计算点积）。这些乘积被加在一起（从数学上来说，一共会有 75 个乘积）。现在你得到了一个数字。切记，该数字只是表示过滤器位于图片左上角的情况。我们在输入内容上的每一位置重复该过程。（下一步将是将过滤器右移 1 单元，接着再右移 1 单元，以此类推。）输入内容上的每一特定位置都会产生一个数字。
过滤器滑过所有位置后将得到一个 28 x 28 x 1 的数组，我们称之为激活映射（activation map）或特征映射（feature map）。之所以得到一个 28 x 28 的数组的原因在于，在一张 32 x 32 的输入图像上，5 x 5 的过滤器能够覆盖到 784 个不同的位置。这 784 个位置可映射为一个 28 x 28 的数组。
当我们使用两个而不是一个 5 x 5 x 3 的过滤器时，输出总量将会变成 28 x 28 x 2。采用的过滤器越多，空间维度（ spatial dimensions）保留得也就越好。
过滤器
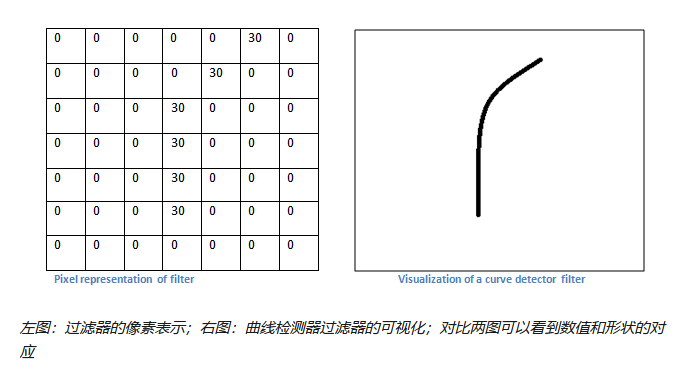
不过，从高层次角度而言卷积是如何工作的？每个过滤器可以被看成是特征标识符（ feature identifiers）。这里的特征指的是例如直边缘、原色、曲线之类的东西。想一想所有图像都共有的一些最简单的特征。假设第一组过滤器是 7 x 7 x 3 的曲线检测器。（在这一节，为了易于分析，暂且忽略该过滤器的深度为 3 个单元，只考虑过滤器和图像的顶层层面。）作为曲线过滤器，它将有一个像素结构，在曲线形状旁时会产生更高的数值（切记，我们所讨论的过滤器不过是一组数值！）
回到数学角度来看这一过程。当我们将过滤器置于输入内容的左上角时，它将计算过滤器和这一区域像素值之间的点积。拿一张需要分类的照片为例，将过滤器放在它的左上角。
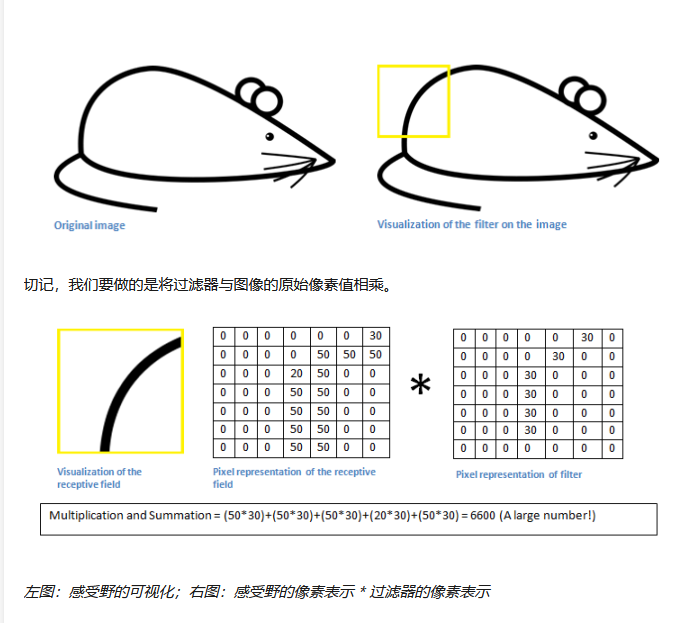
简单来说，如果输入图像上某个形状看起来很像过滤器表示的曲线，那么所有点积加在一起将会得出一个很大的值！让我们看看移动过滤器时会发生什么。
这个值小了很多！这是因为图像的这一部分和曲线检测器过滤器不存在对应。记住，这个卷积层的输出是一个激活映射（activation map）。因此，在这个带有一个过滤器卷积的例子里（当筛选值为曲线检测器），激活映射将会显示出图像里最像曲线的区域。在该例子中，28 x 28 x 1 的激活映射的左上角的值为 6600。高数值意味着很有可能是输入内容中的曲线激活了过滤器。激活地图右上角的值将会是 0，因为输入内容中没有任何东西能激活过滤器（更简单地说，原始图片中的这一区域没有任何曲线）。
这仅仅是一组检测右弯曲线的过滤器。还有其它检测左弯曲线或直线边缘的过滤器。过滤器越多，激活映射的深度越大，我们对输入内容的了解也就越多。
为了预测出图片内容的分类，网络需要识别更高级的特征，例如手、爪子与耳朵的区别。第一个卷积层的输出将会是一个 28 x 28 x 3 的数组（假设我们采用三个 5 x 5 x 3 的过滤器）。当我们进入另一卷积层时，第一个卷积层的输出便是第二个卷积层的输入。
第一层的输入是原始图像，而第二卷积层的输入正是第一层输出的激活映射。也就是说，这一层的输入大体描绘了低级特征在原始图片中的位置。在此基础上再采用一组过滤器（让它通过第 2 个卷积层），输出将是表示了更高级的特征的激活映射。这类特征可以是半圆（曲线和直线的组合）或四边形（几条直线的组合）。随着进入网络越深和经过更多卷积层后，将得到更为复杂特征的激活映射。
形状的抓取
知道了每个filter在做什么之后,我们再来思考这样的一个filter会抓取到什么样的信息。我们知道不同的形状都可由细小的”零件”组合而成的。
比如下图中,用2x2的范围所形成的16种形状可以组合成格式各样的”更大”形状。卷积的每个filter可以探测特定的形状。又由于Feature Map保持了抓取后的空间结构。若将探测到细小图形的Feature Map作为新的输入再次卷积后,则可以由此探测到”更大”的形状概念。比如下图的第一个“大”形状可由2,3,4,5基础形状拼成。第二个可由2,4,5,6组成。第三个可由6,1组成。
除了基础形状之外,颜色、对比度等概念对画面的识别结果也有影响。卷积层也会根据需要去探测特定的概念。
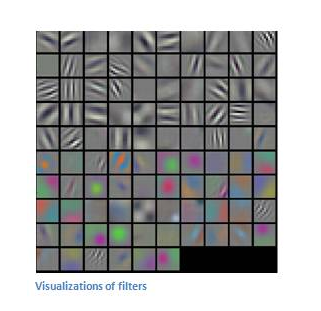
可以从下面这张图中感受到不同数值的filters所卷积过后的Feature Map可以探测边缘,棱角,模糊,突出等概念。
而filter内的权重矩阵W是网络根据数据学习得到的,也就是说,我们让神经网络自己学习以什么样的方式去观察图片。
拿老妇与少女的那幅图片举例,当标签是少女时,卷积网络就会学习抓取可以成少女的形状、概念。当标签是老妇时,卷积网络就会学习抓取可以成老妇的形状、概念。
多个过滤器
每个过滤器可以抓取探测特定的形状的存在。假如我们要探测下图的长方框形状时,可以用4个过滤器去探测4个基础”零件”
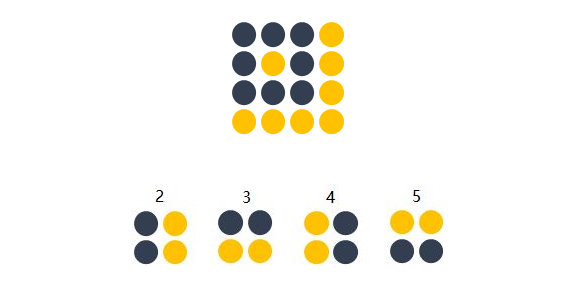
因此我们自然而然的会选择用多个不同的filters对同一个图片进行多次抓取。如下图(动态图过大,如果显示不出,请看到该链接观看) ,同一个图片,经过两个(红色、绿色)不同的filters扫描过后可得到不同特点的Feature Maps,每增加一个filter,就意味着你想让网络多抓取一个特征。
这样卷积层的输出也不再是depth为1的一个平面,而是和输入一样是depth为复数的长方体。
如下图所示,当我们增加一个filter (紫色表示)后,就又可以得到一个Feature Map。将不同filters所卷积得到的Feature Maps按顺序堆叠后,就得到了一个卷积层的最终输出。
这样卷积后输出的长方体可以作为新的输入送入另一个卷积层中处理。
加入非线性
和前馈神经网络一样,经过线性组合和偏移后,会加入非线性增强模型的拟合能力。
将卷积所得的Feature Map经过ReLU变换(elementwise)后所得到的output就如下图所展示。
完全连接层
检测高级特征之后，网络最后的完全连接层就更是锦上添花了。简单地说，这一层处理输入内容（该输入可能是卷积层、ReLU 层或是池化层的输出）后会输出一个 N 维向量，N 是该程序必须选择的分类数量。例如，如果你想得到一个数字分类程序，如果有 10 个数字，N 就等于 10。这个 N 维向量中的每一数字都代表某一特定类别的概率。例如，如果某一数字分类程序的结果矢量是 [0 .1 .1 .75 0 0 0 0 0 .05]，则代表该图片有 10% 的概率是 1、10% 的概率是 2、75% 的概率是 3、还有 5% 的概率是 9（注：还有其他表现输出的方式，这里只展示了 softmax 的方法）。
完全连接层观察上一层的输出（其表示了更高级特征的激活映射）并确定这些特征与哪一分类最为吻合。例如，如果该程序预测某一图像的内容为狗，那么激活映射中的高数值便会代表一些爪子或四条腿之类的高级特征。同样地，如果程序测定某一图片的内容为鸟，激活映射中的高数值便会代表诸如翅膀或鸟喙之类的高级特征。大体上来说，完全连接层观察高级特征和哪一分类最为吻合和拥有怎样的特定权重，因此当计算出权重与先前层之间的点积后，你将得到不同分类的正确概率。
步幅和填充
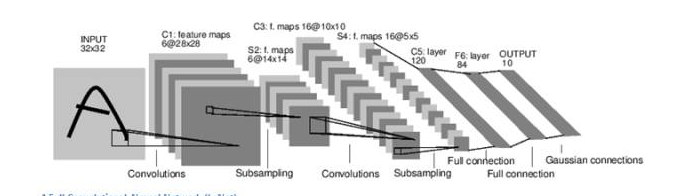
选择了过滤器的尺寸以后，我们还需要选择步幅（stride）和填充（padding）。
步长
步幅控制着过滤器围绕输入内容进行卷积计算的方式。在第一部分我们举的例子中，过滤器通过每次移动一个单元的方式对输入内容进行卷积。过滤器移动的距离就是步幅。在那个例子中，步幅被默认设置为1。步幅的设置通常要确保输出内容是一个整数而非分数。让我们看一个例子。想象一个 7 x 7 的输入图像，一个 3 x 3 过滤器（简单起见不考虑第三个维度），步幅为 1。这是一种惯常的情况。
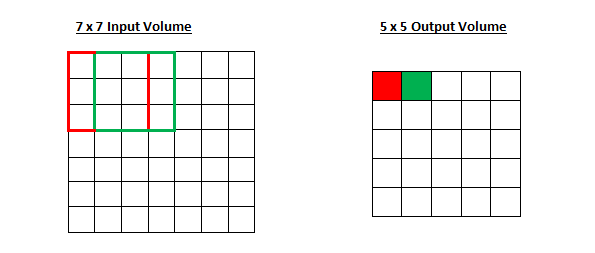
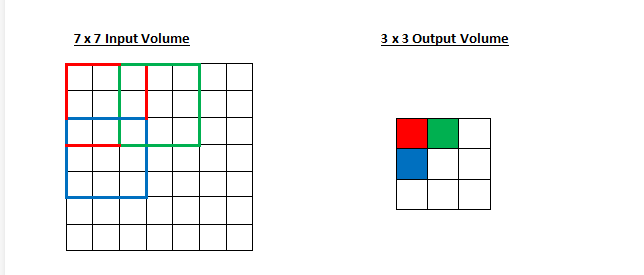
感受野移动了两个单元，输出内容同样也会减小。注意，如果试图把我们的步幅设置成 3，那我们就会难以调节间距并确保感受野与输入图像匹配。正常情况下，程序员如果想让接受域重叠得更少并且想要更小的空间维度（spatial dimensions）时，他们会增加步幅。
填充
现在让我们看一下填充（padding）。在此之前，想象一个场景：当你把 5 x 5 x 3 的过滤器用在 32 x 32 x 3 的输入上时，会发生什么？输出的大小会是 28 x 28 x 3。注意，这里空间维度减小了。如果我们继续用卷积层，尺寸减小的速度就会超过我们的期望。
在网络的早期层中，我们想要尽可能多地保留原始输入内容的信息，这样我们就能提取出那些低层的特征。比如说我们想要应用同样的卷积层，但又想让输出量维持为 32 x 32 x 3 。为做到这点，我们可以对这个层应用大小为 2 的零填充（zero padding）。零填充在输入内容的边界周围补充零。如果我们用两个零填充，就会得到一个 36 x 36 x 3 的输入卷。
池化层
在几个 ReLU 层之后，程序员也许会选择用一个池化层（pooling layer）。它同时也被叫做下采样（downsampling）层。在这个类别中，也有几种可供选择的层，最受欢迎的就是最大池化（ max-pooling）。它基本上采用了一个过滤器（通常是 2x2 的）和一个同样长度的步幅。然后把它应用到输入内容上，输出过滤器卷积计算的每个子区域中的最大数字。
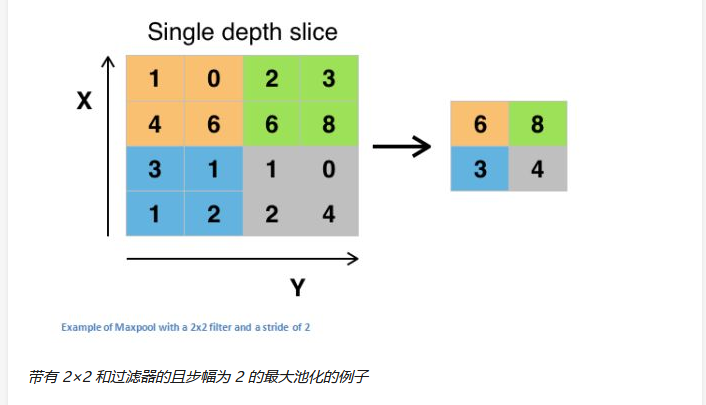
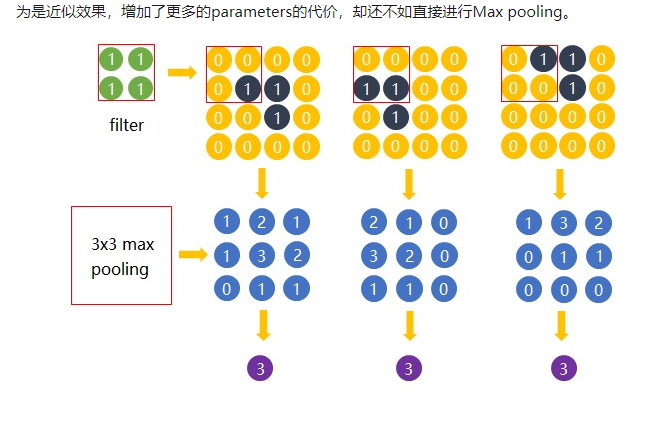
Max pooling的主要功能是downsampling,却不会损坏识别结果。这意味着卷积后的FeatureMap中有对于识别物体不必要的冗余信息。那么我们就反过来思考,这些”冗”信息是如何产生的。
直觉上,我们为了探测到某个特定形状的存在,用一个filer对整个图片进行逐步扫描。但只有出现了该特定形状的区域所卷积获得的输出才是真正有用的,用该filter卷积其他区域得出的数值就可能对该形状是否存在的判定影响较小。
比如下图中,我们还是考虑探测”横折”这个形状。卷积后得到3x3的Feature Map中,真正有用的就是数字为3的那个节点,其余数值对于这个任务而言都是无关的。所以用3x3的Max pooling后,并没有对“横折”的探测产生影响。试想在这里例子中如果不使用Max pooling,而让网络自己去学习。网络也会去学习与Max pooling近似效果的权重。因为是近似效果,增加了更多的parameters的代价,却还不如直接进行Max pooling
池化层还有其他选择，比如平均池化（average pooling）和 L2-norm 池化 。这一层背后的直观推理是：一旦我们知道了原始输入（这里会有一个高激活值）中一个特定的特征，它与其它特征的相对位置就比它的绝对位置更重要。可想而知，这一层大幅减小了输入卷的空间维度（长度和宽度改变了，但深度没变）。
这到达了两个主要目的。第一个是权重参数的数目减少到了75%，因此降低了计算成本。第二是它可以控制过拟合（overfitting）。这个术语是指一个模型与训练样本太过匹配了，以至于用于验证和检测组时无法产生出好的结果。出现过拟合的表现是一个模型在训练集能达到 100% 或 99% 的准确度，而在测试数据上却只有50%。
数据增强技术
如何利用一些简单的转换方法将你现有的数据集变得更大。正如我们之前所提及的，当计算机将图片当作输入时，它将用一个包含一列像素值的数组描述（这幅图）。若是图片左移一个像素。对你和我来说，这种变化是微不可察的。然而对计算机而已，这种变化非常显著：这幅图的类别和标签保持不变，数组却变化了。
这种改变训练数据的数组表征而保持标签不变的方法被称作数据增强技术。这是一种人工扩展数据集的方法。人们经常使用的增强方法包括灰度变化、水平翻转、垂直翻转、随机编组、色值跳变、翻译、旋转等其他多种方法。通过利用这些训练数据的转换方法，你将获得两倍甚至三倍于原数据的训练样本。
FCN(全卷积网络)(Fully Convolutional Network)
分割(语义，实例，全景分割)
分割，顾名思义，就是把一个完整的东西按照某种方式或规则分成若干个部分。
那么什么是图像分割呢？简单来说，就是把图像中属于同一类别或同一个体的东西划分在一起，并将各个子部分区分开来。像下图这样：
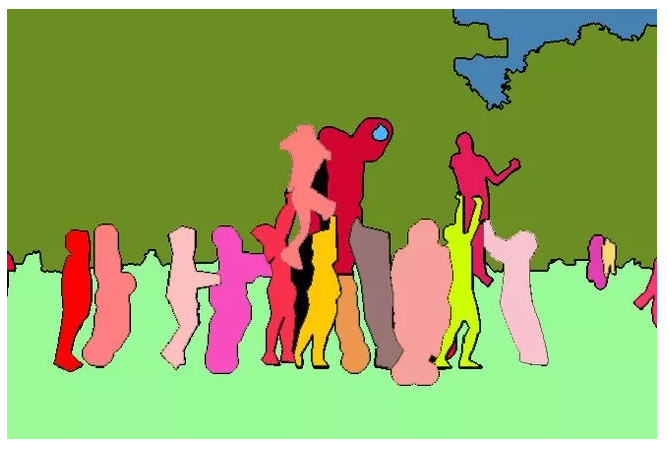
为了训练神经网络，图片中这些像素点会按照某种规则被贴上一个“标签”，比如这个像素点是属于人、天空、草地还是树；更详细一点，可以再给它们第二个标签，声明它们是属于“哪一个人”或“哪一棵树”。
对于只有一个标签的（只区分类别）的任务，我们称之为“语义分割”（semantic segmentation）；
对于区分相同类别的不同个体的，则称之为实例分割（instance segmentation）。
由于实例分割往往只能分辨可数目标，因此，为了同时实现实例分割与不可数类别的语义分割，2018年Alexander Kirillov等人提出了全景分割（panoptic segmentation）的概念。
下图分别展示了（a）原始图像，（b）语义分割，（c）实例分割和（d）全景分割。
语义分割
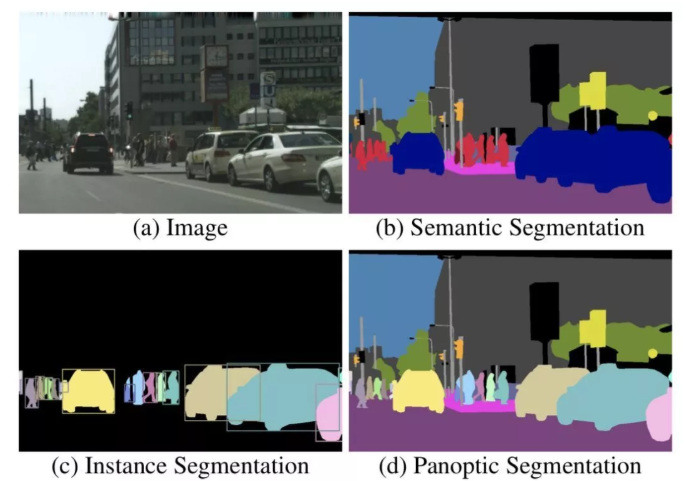
图像语义分割(Semantic Segmentation)是图像处理和是机器视觉技术中关于图像理解的重要一环，也是 AI 领域中一个重要的分支。语义分割即是对图像中每一个像素点进行分类，确定每个点的类别（如属于背景、人或车等），从而进行区域划分。目前，语义分割已经被广泛应用于自动驾驶、无人机落点判定等场景中。
截止目前，CNN已经在图像分类分方面取得了巨大的成就，涌现出如VGG和Resnet等网络结构，并在ImageNet中取得了好成绩。CNN的强大之处在于它的多层结构能自动学习特征，并且可以学习到多个层次的特征：
这些抽象特征对物体的大小、位置和方向等敏感性更低，从而有助于分类性能的提高。这些抽象的特征对分类很有帮助，可以很好地判断出一幅图像中包含什么类别的物体。图像分类是图像级别的！
与分类不同的是，语义分割需要判断图像每个像素点的类别，进行精确分割。图像语义分割是像素级别的！但是由于CNN在进行convolution和pooling过程中丢失了图像细节，即feature map size逐渐变小，所以不能很好地指出物体的具体轮廓、指出每个像素具体属于哪个物体，无法做到精确的分割。
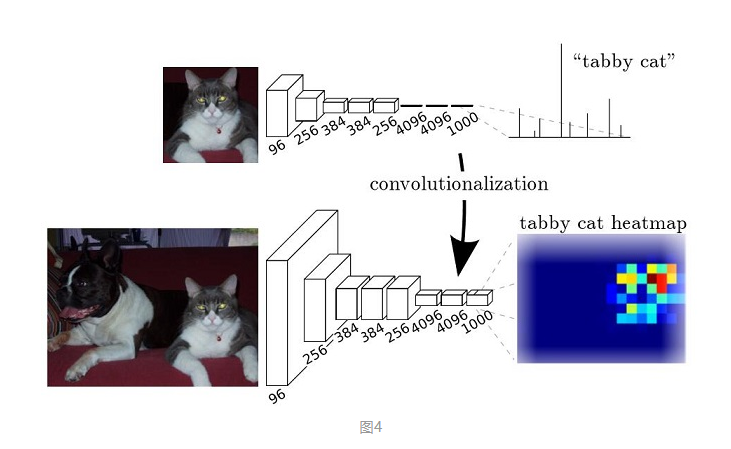
针对这个问题，Jonathan Long等人提出了Fully Convolutional Networks（FCN）用于图像语义分割。自从提出后，FCN已经成为语义分割的基本框架，后续算法其实都是在这个框架中改进而来。
FCN与CNN区别
对于一般的分类CNN网络，如VGG和Resnet，都会在网络的最后加入一些全连接层，经过softmax后就可以获得类别概率信息。但是这个概率信息是1维的，即只能标识整个图片的类别，不能标识每个像素点的类别，所以这种全连接方法不适用于图像分割。
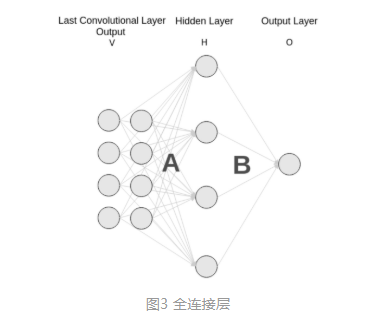
而FCN提出可以把后面几个全连接都换成卷积，这样就可以获得一张2维的feature map，后接softmax获得每个像素点的分类信息，从而解决了分割问题，如图4。
反卷积与上采样
上采样（upsampling）一般包括2种方式：
- Resize，如双线性插值直接缩放，类似于图像缩放
- Deconvolution，也叫Transposed Convolution
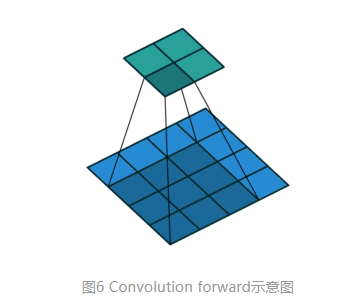
对于一般卷积，输入蓝色4x4矩阵，卷积核大小3x3。当设置卷积参数pad=0，stride=1时，卷积输出绿色2x2矩阵，如图6。
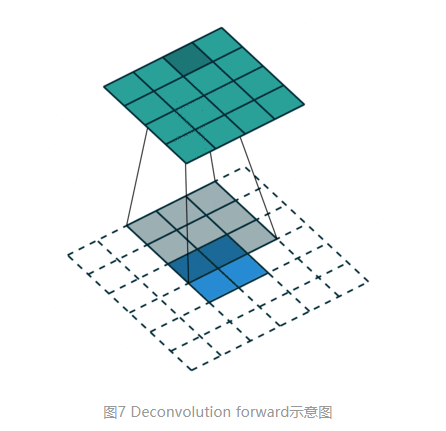
而对于反卷积，相当于把普通卷积反过来，输入蓝色2x2矩阵（周围填0变成6x6），卷积核大小还是3x3。当设置反卷积参数pad=0，stride=1时输出绿色4x4矩阵，如图7，这相当于完全将图4倒过来
传统的网络是subsampling的，对应的输出尺寸会降低；upsampling的意义在于将小尺寸的高维度feature map恢复回去，以便做pixelwise prediction，获得每个点的分类信息。
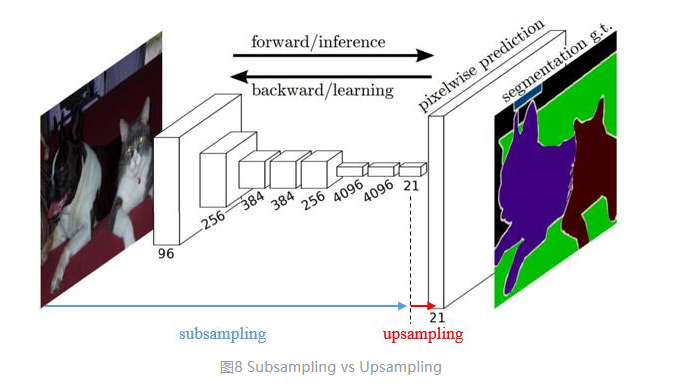
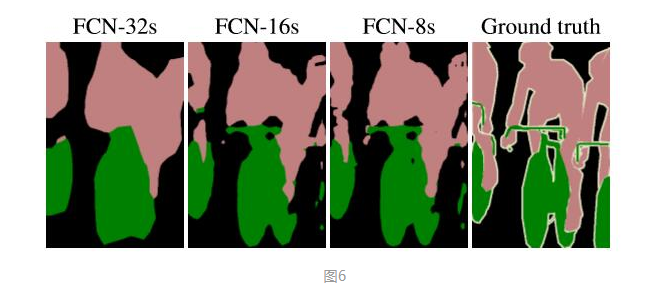
上采样在FCN网络中的作用如图8，明显可以看到经过上采样后恢复了较大的pixelwise feature map，这其实相当于一个Encode-Decode的过程。 （编码和解码
FCN的缺陷
- 无法解决实例分割问题
- 速度远不能达到实时
- 不能够应对诸如3D点云等不定型数据
U-Net
U-Net是一种分割网络，能够适应很小的训练集（大约30张图）。
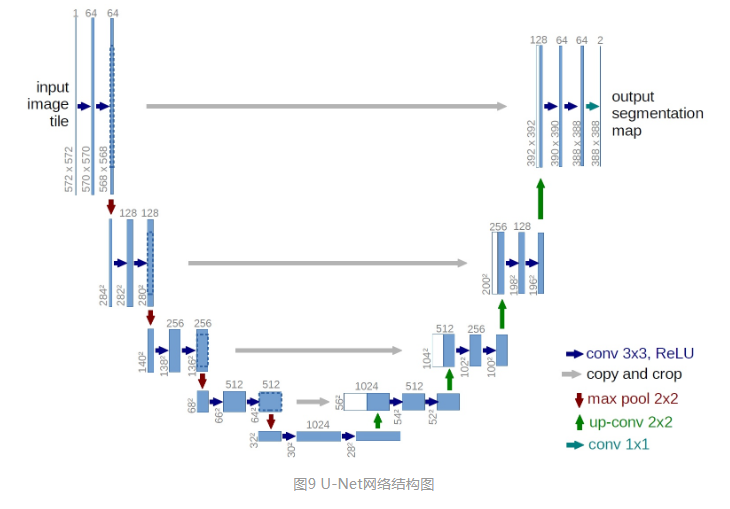
整个U-Net网络结构如图9，类似于一个大大的U字母：首先进行Conv+Pooling下采样；然后Deconv反卷积进行上采样，crop之前的低层feature map，进行融合；然后再次上采样。重复这个过程，直到获得输出388x388x2的feature map，最后经过softmax获得output segment map。总体来说与FCN思路非常类似。
Unet 网络结构是对称的，形似英文字母 U 所以被称为 Unet。整张图都是由蓝/白色框与各种颜色的箭头组成，其中，蓝/白色框表示 feature map；蓝色箭头表示 3x3 卷积，用于特征提取；灰色箭头表示 skip-connection，用于特征融合；红色箭头表示池化 pooling，用于降低维度；绿色箭头表示上采样 upsample，用于恢复维度；青色箭头表示 1x1 卷积，用于输出结果。
U-Net采用了与FCN完全不同的特征融合方式：拼接！
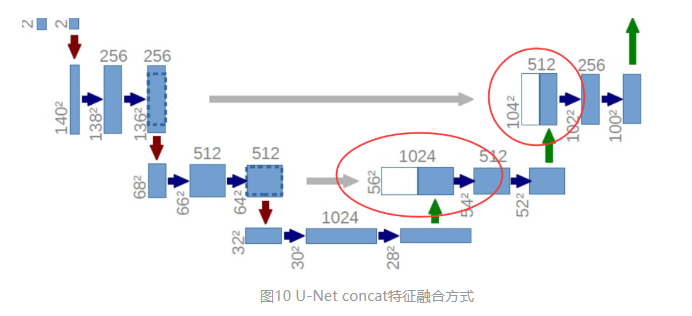
与FCN逐点相加不同，U-Net采用将特征在channel维度拼接在一起，形成更“厚”的特征。所以：
两种特征融合方法
语义分割网络在特征融合时也有2种办法：
- FCN式的逐点相加，
- U-Net式的channel维度拼接融合
运用CNN的分割问题上，主要分为以FCN为基础的结构，和以U-Net为基础的结构。前者的encoder-decoder是非对称的，后者的encoder-decoder是对称的；
U-Net为何适用于医学图像
医学图像特点
- 图像语义较为简单、结构较为固定。我们做脑的，就用脑CT和脑MRI，做胸片的只用胸片CT，做眼底的只用眼底OCT，都是一个固定的器官的成像。由于器官本身结构固定和语义信息没有特别丰富，所以高级语义信息和低级特征都显得很重要(UNet的skip connection和U型结构就派上了用场)。
- 数据量少。医学影像的数据获取相对难一些，很多比赛只提供不到100例数据。所以我们设计的模型不宜过大，如果参数过多，很容易导致过拟合。
- 多模态。相比自然影像，医疗影像比较有趣和不同的一点是，医疗影像是具有多种模态的。以ISLES脑梗竞赛为例，其官方提供了CBF,MTT,CBV,TMAX,CTP等多种模态的数据。这就需要我们更好的设计网络去提取不同模态的特征feature。。
- 可解释性重要。由于医疗影像最终是辅助医生的临床诊断，所以网络告诉医生一个3D的CT有没有病是远远不够的，医生还要进一步的想知道，病灶在哪一层，在哪一层的哪个位置，分割出来了吗，能求体积嘛？同时对于网络给出的分类和分割等结果，医生还想知道为什么，也就是说从医生角度出发，更希望知道医疗AI的可解释性如何
解释医学影像以Attention及CAM(class-activation-map)等可视化方法为主。
因为医学图像边界模糊、梯度复杂，需要较多的高分辨率信息。高分辨率用于精准分割。
人体内部结构相对固定，分割目标在人体图像中的分布很具有规律，语义简单明确，低分辨率信息能够提供这一信息，用于目标物体的识别。
UNet结合了低分辨率信息（提供物体类别识别依据）和高分辨率信息（提供精准分割定位依据），完美适用于医学图像分割。
Seg-Net
解码器
分割任务中的编码器encode与解码器decode就像是玩“你来比划我来猜”的双方：比划的人想把看到的东西用一种方式描述出来，猜的人根据比划的人提供的信息猜出答案。
其中，“比划的人”叫做编码器，“猜的人”就是解码器。
具体来说，编码器的任务是在给定输入图像后，通过神经网络学习得到输入图像的特征图谱；而解码器则在编码器提供特征图后，逐步实现每个像素的类别标注，也就是分割。
通常，分割任务中的编码器结构比较类似，大多来源于用于分类任务的网络结构，比如VGG。这样做有一个好处，就是可以借用在大数据库下训练得到的分类网络的权重参数，通过迁移学习实现更好的效果。因此，解码器的不同在很大程度上决定了一个基于编解码结构的分割网络的效果。
SegNet的编码器结构与解码器结构是一一对应的，即一个decoder具有与其对应的encoder相同的空间尺寸和通道数。对于基础SegNet结构，二者各有13个卷积层，其中编码器的卷积层就对应了VGG16网络结构中的前13个卷积层。
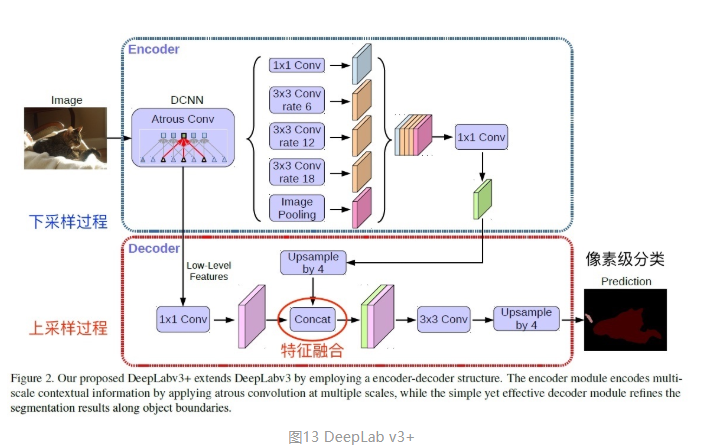
下图是SegNet的网络结构，其中蓝色代表卷积+Batch Normalization+ReLU，绿色代表max-pooling，红色代表上采样，黄色是Softmax。
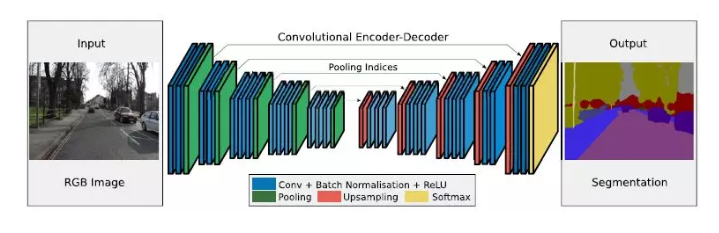
SegNet与FCN的对应结构相比，体量要小很多。这主要得益于SegNet中为了权衡计算量而采取的操作：用记录的池化过程的位置信息替代直接的反卷积操作。具体如下图所示。
Seg-Net与FCN解码方式的不同
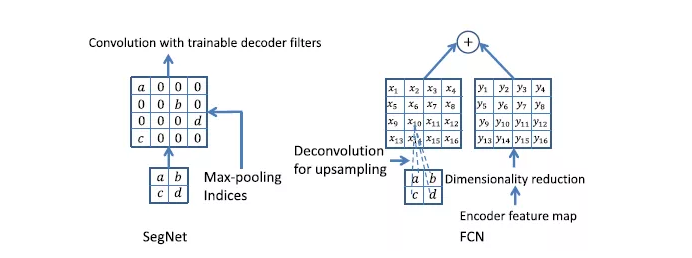
图中左侧是SegNet使用的解码方式，右侧是FCN对应的解码方式。可以看到，SegNet的做法是先根据位置信息生成稀疏的特征图，再利用后续的卷积计算恢复稠密特征图。而FCN则直接利用反卷积操作求得上采样后的特征图，再将其与编码器特征图相加。
改变解码器的参数
前文已经提到，编解码结构中，解码器的效果和复杂程度对于整个分割网络的影响是非常大的。这里我们就一起来看一下不同解码器结构和它们的效果。
SegNet中一共尝试了8种不同的解码结构，先上结果：
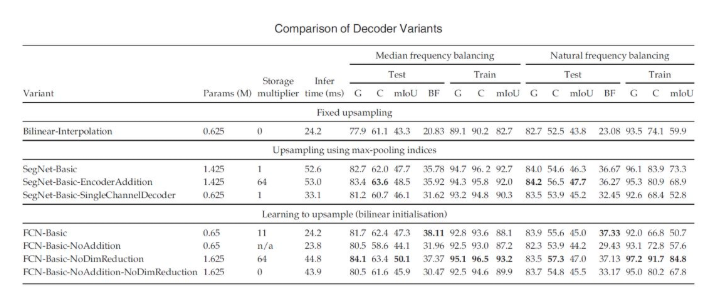
这些变体共用相同的编码器结构，只是在解码器结构上有所不同。比如，将解码器的结构单纯减少层数，改变解码器最后一层通道数，改变编解码器对应结构之间的连接方式（只连接池化信息、保留特征层内信息或全部保留），改变采样方式等。
除上面几种变体外，论文中还尝试了改变上采样方法，或取消池化和下采样过程，但是这些改变都没有带来更好的结果。
解码器总结
- 保留编码器所有特征图所实现的效果最好，在这一点上语义分割边缘轮廓描述度量（BF）体现最为明显。
- 当推理过程的内存受限时，可以使用编码器特征图的压缩形式（比如缩小维度、使用池化信息等），但需要搭配合适的解码器形式（比如SegNet类型的）来提升表现。
- 在给定编码器时，越大的解码器效果越好。
图像处理的非深度学习方法
图像分割是什么？如果下学术定义，就是把图像分割成想要的语义上相同的若干子区域，看上面的自动驾驶的分割任务，路是路，车是车，树是树。
这些子区域，组成图像的完备子集，相互之间不重叠。图像分割可以被看作是一个逐像素的图像分类问题
没有深度学习的那些年，也发展出了非常多的图像分割技术。
边缘与阈值法
简单的边缘检测也曾被用于图像分割，但是因为要做复杂后处理以及后面和其他方法有重叠，这里就不再说了，而是从阈值法开始说。
阈值法的基本思想是基于图像的灰度特征来计算一个或多个灰度阈值，并将图像中每个像素的灰度值与阈值相比较。
其中，最广泛使用也最具有代表性质就是OTSU【1】方法，它是用于灰度图像分割的方法，核心思想就是使类间方差最大。
这样的方法，非常简单，要求被分割的物体颜色纹理比较紧凑，类内方差小，只适合一些文本图像的处理，比如车牌，比如指纹。
区域增长，分裂
阈值法的一个硬伤是太粗暴简单，哪怕是自适应的局部阈值法，一样难逃无法分割类内方差较大的目标的宿命。它完全没有利用好像素的空间信息，导致分割结果极其容易受噪声干扰，经常出现断裂的边缘，需要后处理。
所以，区域生长法出现了，它通过一些种子点，再加上相似性准则来不断扩充区域直到达到类别的边界，这时候分割结果是连续的了。
区域分裂则是反过程，不再详述。区域增长法的佼佼者，就是分水岭算法【2】。
分水岭算法是一种基于拓扑理论的数学形态学的分割方法，将图像中每一点像素的灰度值表示该点的海拔高度，每一个局部极小值称为集水盆，而集水盆的边界则是分水岭。分水岭算法有很多种实现算法，常用浸水模拟法。
分水岭算法对于弱边缘有不错的响应，因此常被用于材料图像的分割，以及产生超像素用于提高其他方法的分割效率。咱在硕士期间也与师姐鼓捣过半导体材料的分割，还不错。
说到这里，超像素也是很重要的一种方法，某种程度上也能被归为图像分割的方法。SLIC，Meanshift等都是非常经典的方法，去文【3】中做更详细解读吧。
图割
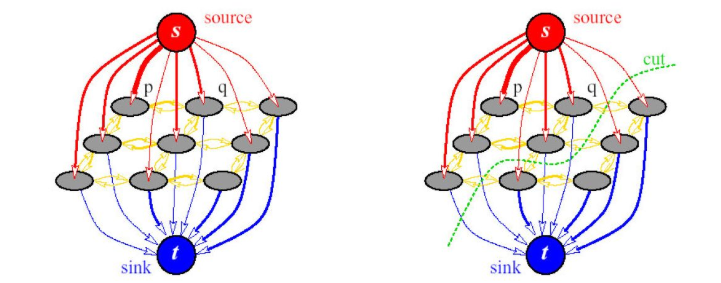
以graphcut【4】为代表的图割方法，是传统图像分割里面鲁棒性最好的方法，它是一种概率无向图模型(Probabilistic undirected graphical model)，又被称Markov random field马尔可夫随机场。
Graphcut的基本思路，就是建立一张图，看下面这张图，其中以图像像素或者超像素作为图像顶点，然后优化的目标就是要找到一个切割，使得各个子图不相连从而实现分割，前提是移除边的和权重最小。
后来图割方法从MRF发展到CRF，也就是条件随机场。它通常包含两个优化目标，一个是区域的相似度，被称为区域能量项，即piecewise能量。一个是被切断边的相似度，被称为边缘能量项，即pairwise能量。它追求区域能量项的最大化以及边缘能量的最小化，也就是区域内部越相似越好，区域间相似度越低越好。
图割方法很通用，对于纹理比较复杂的图像分割效果也不错。缺点是时间复杂度和空间复杂度较高，所以通常使用超像素进行加速计算，上面的分水岭算法就可以拿来用用。
graphcut的迭代版本，也就是grabcut【5】更好用，它的基本思路是；使用混合高斯**模型(Gaussian Mixture Model，GMM)**替代了graphcut基于灰度的模型，初始的混合高斯模型的构建，通过用户交互来指定，只需要指定确定性的背景像素区域即可，通常是画一个框。
多年以后再看下面这张图，效果依然是惊艳的，边缘很不错。不像上面的几个方法，图割方法仍然被广泛使用，deeplab系列的前几篇文章就用到了全连接的crf，它与mrf的区别可以参考这篇文章【Discriminative fields for modeling spatial dependencies in natural images】。
轮廓模型
轮廓模型大部分人可能不知道，它的基本思想是使用连续曲线来表达目标轮廓，并定义一个能量泛函，其自变量为曲线，将分割过程转变为求解能量泛函的最小值的过程。数值实现可通过求解函数对应的欧拉(Euler-Lagrange)方程来实现。包括以snake模型为代表的参数活动轮廓模型和以水平集方法为代表的几何活动轮廓模型。
当能量达到最小时的，曲线位置就处于正确的目标轮廓。
该类分割方法具有几个显著的特点：(1)由于能量泛函是在连续状态下实现，所以最终得到的图像轮廓可以达到较高的精度；(2)通过约束目标轮廓为光滑，同时融入其它关于目标形状的先验信息，算法可以具有较强的鲁棒性；(3)使用光滑的闭合曲线表示物体的轮廓，可获取完整的轮廓，从而避免传统图像分割方法中的预/后处理过程。
不过，缺点也很明显，比较敏感，容易陷入局部极值。
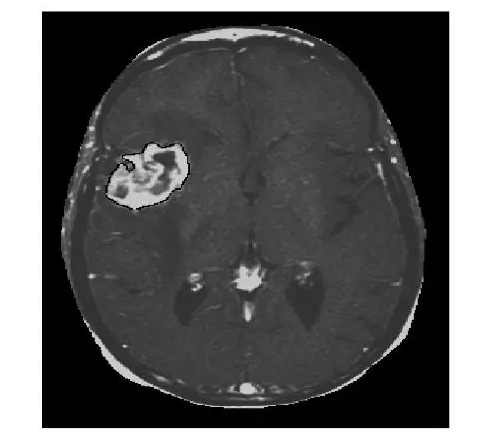
下面是我的硕士论文【6】中采用水平集方法分割出的肿瘤，就是白色那一块。这个方法的数学味有点浓，考虑到咱们是闲聊，就不摆公式了，毕竟后面还有很多事。
参考
共形几何第四节-不动点，庞加莱-霍普斯定理
布劳威尔(Brouwer)不动点理论
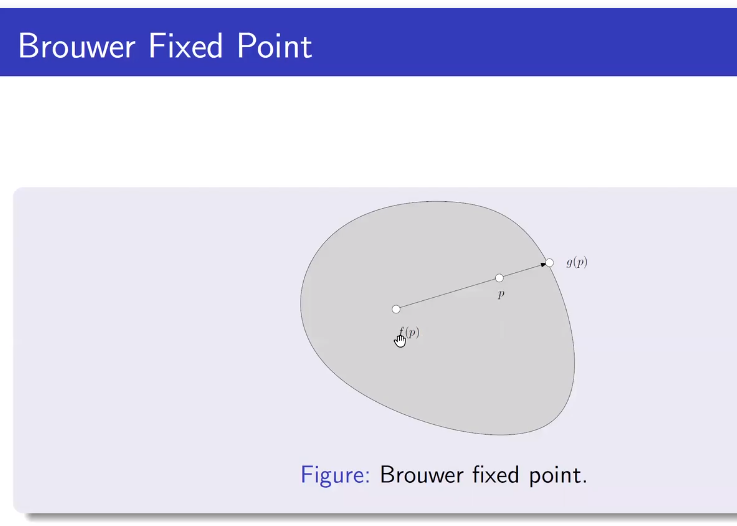
对于一个拓扑空间中满足一定条件的连续函数f，存在一个点x0，使得f(x0) = x0。
这个定理可以通过很实际的例子来理解。比如：取两张一样大小的白纸，在上面画好垂直的坐标系以及纵横的方格。将一张纸平铺在桌面，而另外一张随意揉成一个形状（但不能撕裂），放在第一张白纸之上，不超出第一张的边界。那么第二张纸上一定有一点正好就在第一张纸的对应点的正上方。一个更简单的说法是：将一张白纸平铺在桌面上，再将它揉成一团（不撕裂），放在原来白纸所在的地方，那么只要它不超出原来白纸平铺时的边界，那么白纸上一定有一点在水平方向上没有移动过。
这个断言的根据就是布劳威尔不动点定理在二维欧几里得空间（欧几里得平面）的情况，因为把纸揉皱是一个连续的变换过程。
另一个例子是大商场等地方可以看到的平面地图，上面标有“您在此处”的红点。如果标注足够精确，那么这个点就是把实际地形射到地图的连续函数的不动点。
地球绕着它的自转轴自转。自转轴在自转过程中是不变的，也就是自转运动的不动点
如果我们用一个密封的锅子煮水，那么总有一个水分子在煮开前的某一刻和煮开后的某一刻处于同样的位置。
共形几何第三节-同调群和上同调群Homology and Cohomology
计算共形几何2-基础群和覆盖空间
计算共形几何笔记-1
如何制作一张地图？
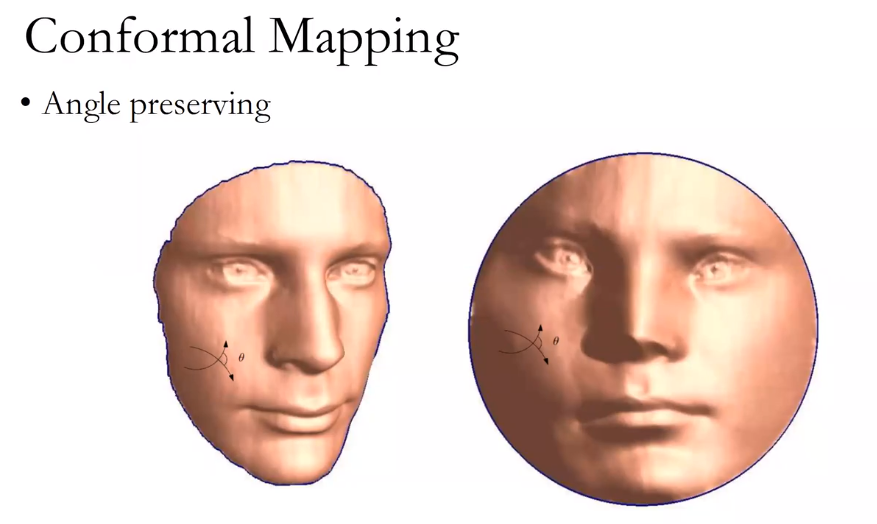
怎么样做一个地球的平面图？很难，就像把橘子皮摊平一样，如果没有扭曲和切割几乎不可能。
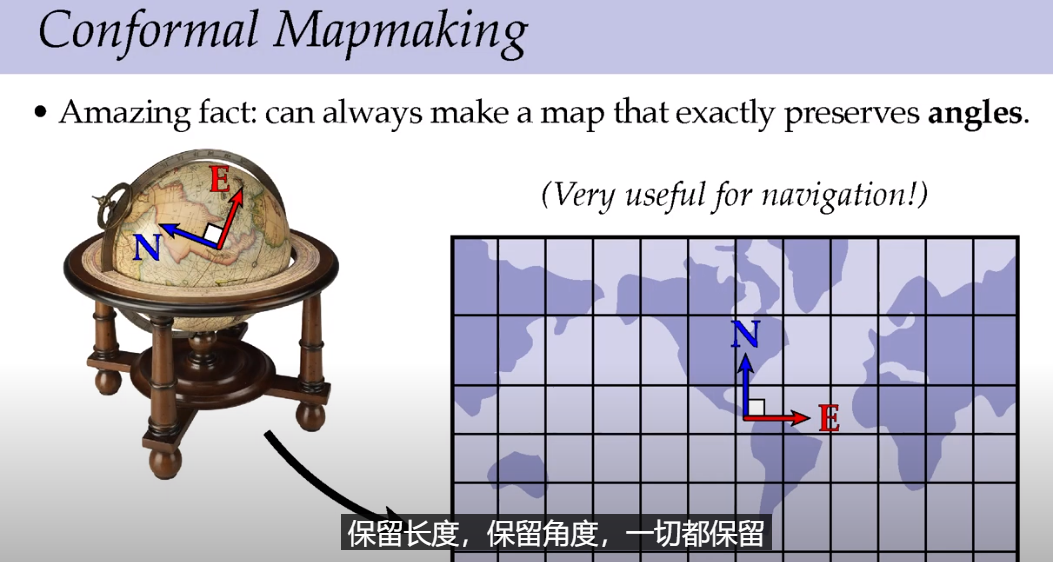
既然不能尺寸和角度不能都保留，那么共形几何选择在绘制地图的时候保持角度，在航海地图的时候很有用。
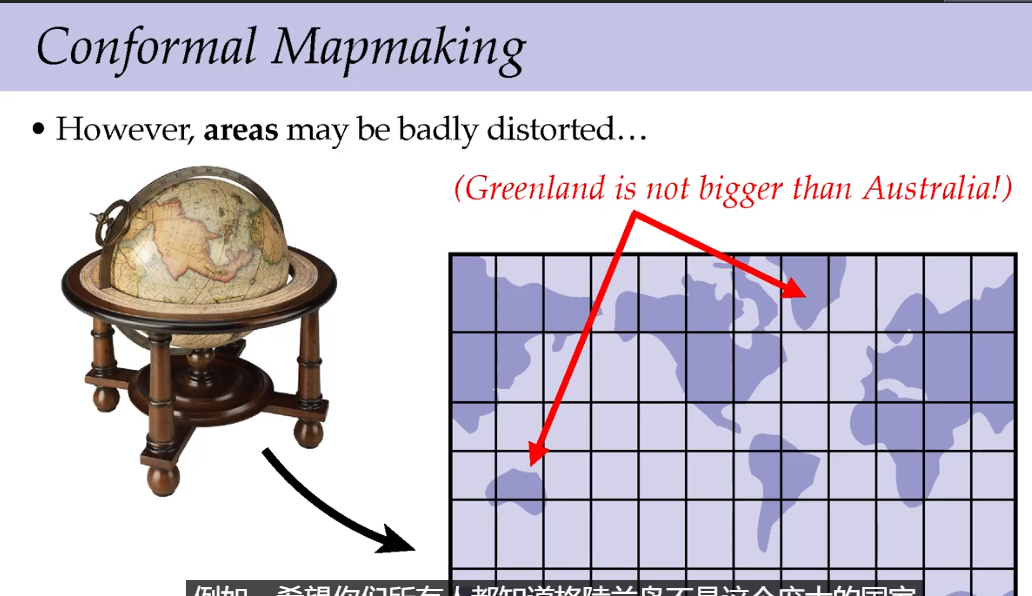
保留角度会使得地图上一些区域的面积严重扭曲，例如在地图上看，格陵兰岛面积比澳大利亚大，但是实际上澳大利亚面积768万平方千米，是世界上最小的大陆；格陵兰岛面积216万平方千米，是世界上最大的岛屿。澳大利亚的实际面积相当于格陵兰岛的三倍多。
经过将球体地图投影到平面上，角度得到了保留，但是局部的尺寸和比例发生了严重的变化。
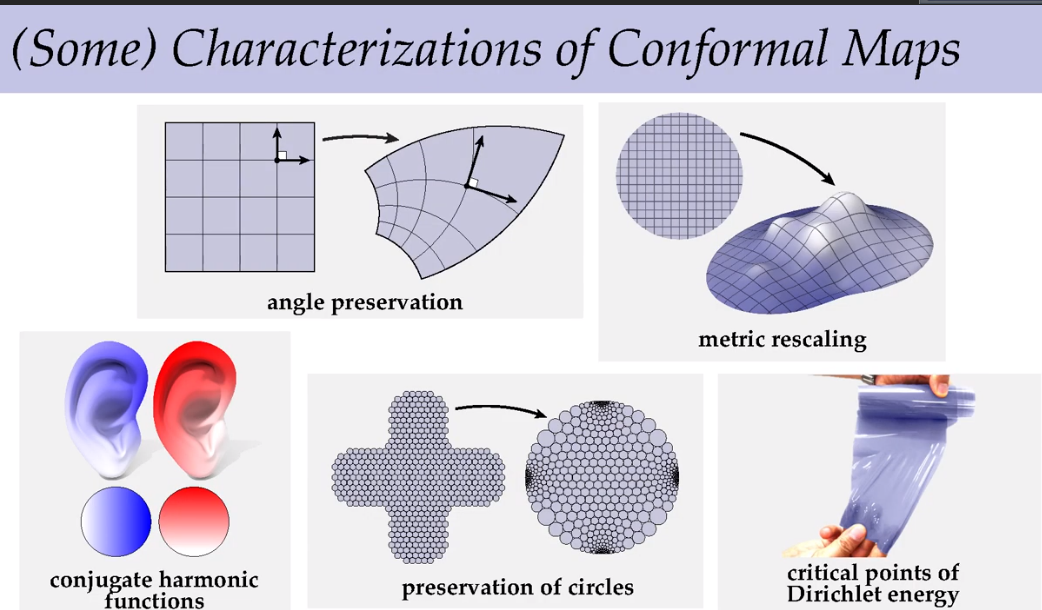
一般来讲，共型几何研究的是保持角度。
为何保持角度？
那为什么要保持角度不变，即共形？
计算效率和几何处理效率更高。
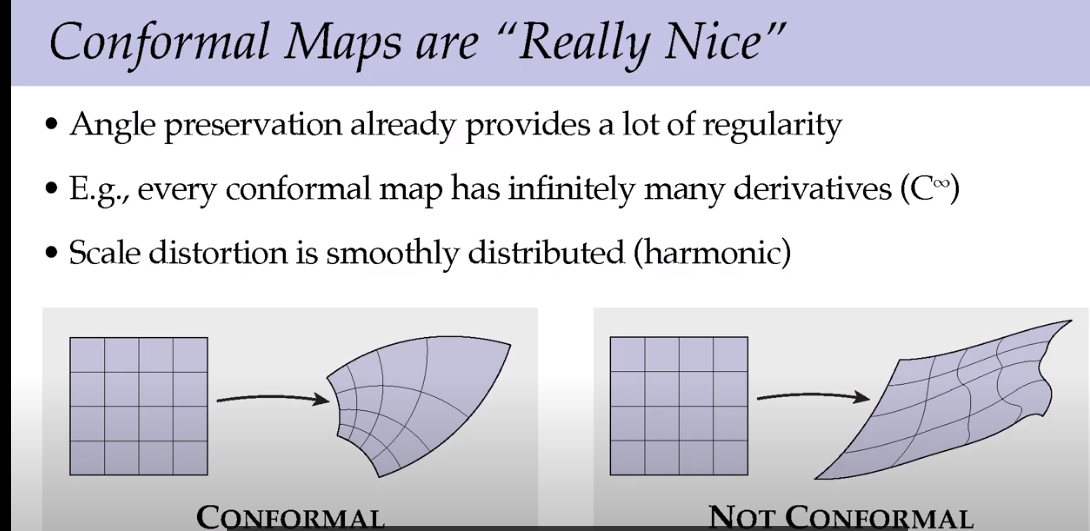
尺寸变化非常平滑。
假设在地球上旅行，可以不用思考角度问题，而只考虑尺寸，这样简化了问题。
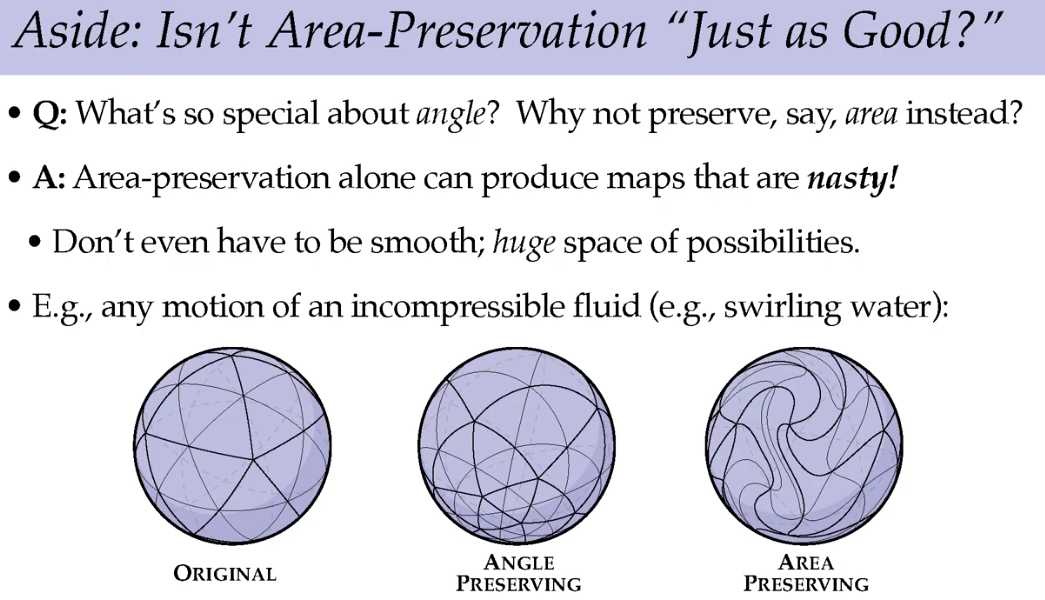
那为什么不保留面积？保留面积产生的图形极为复杂难懂，也不平滑。
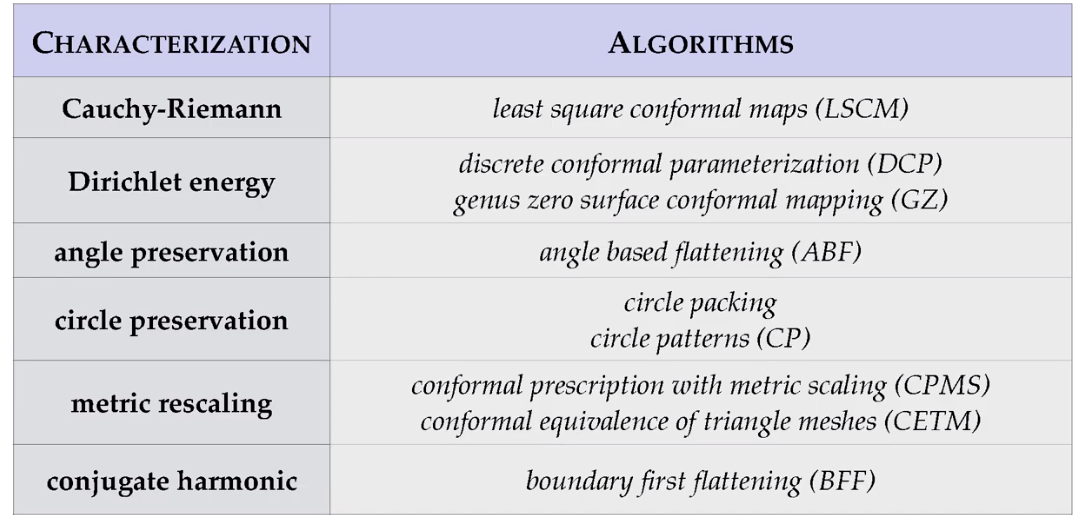
共形几何可以解决很多问题。
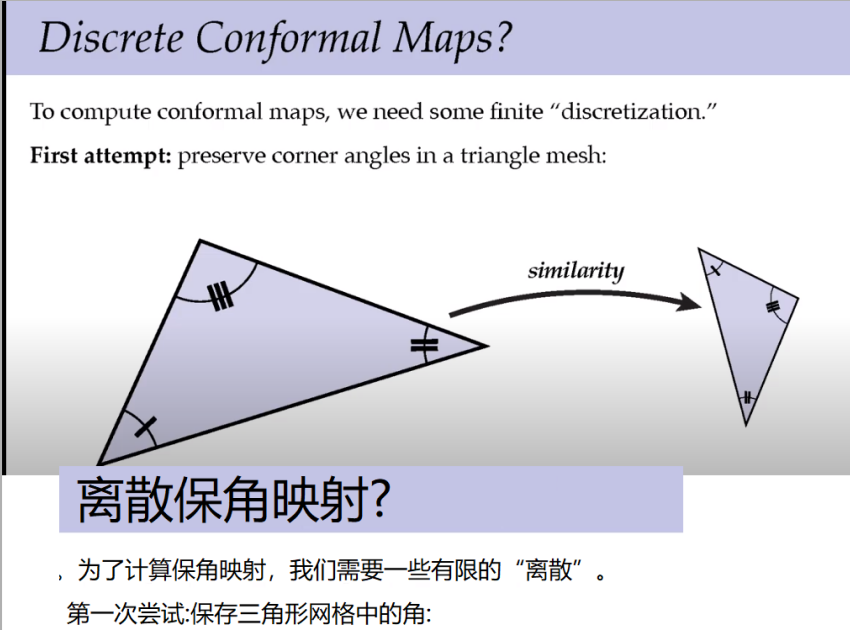
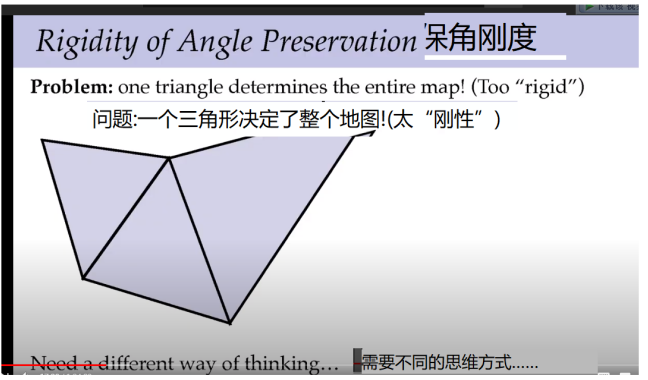
一旦把第一个三角形保留了角度，其他的都不能变了。结果已经固定，这时候需要一些别的思考方式。
曲面的保角映射
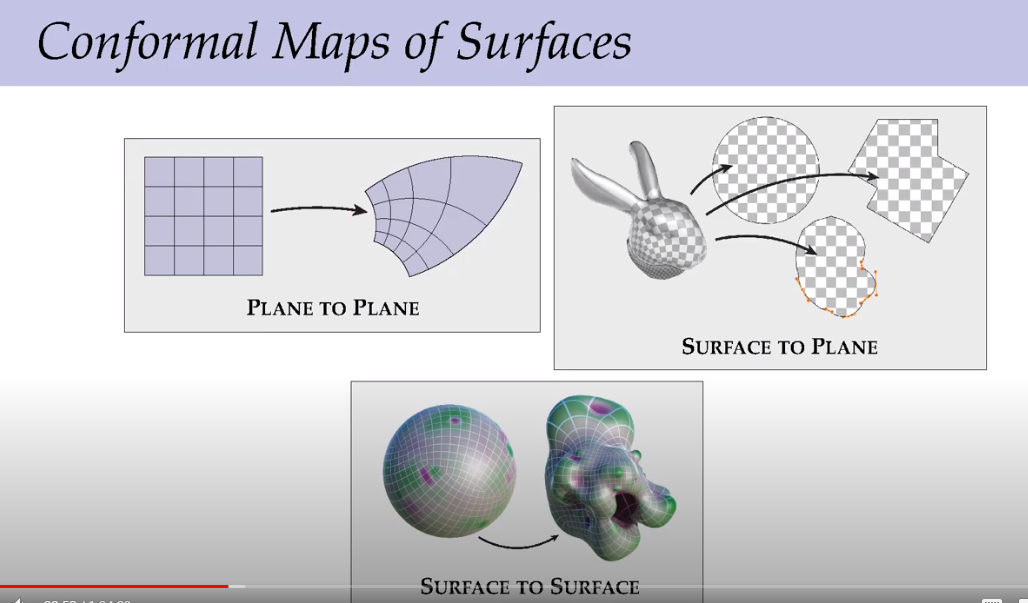
把雕像展为2维平面和制作一幅地图的过程是一样的。
如果在平面上绘制小圆，则经过变换之后的3维空间中的圆形则会保持角度，但大小会发生扭曲，变成椭圆。
共形映射补充(2020-11-8)
来源:复变函数与积分变换 华中科技大学 MOOC 尹慧 第六章共形映射
伸缩率的概念
旋转角的概念
导数的几何意义
我TM直接爆炸草？
单值化定理
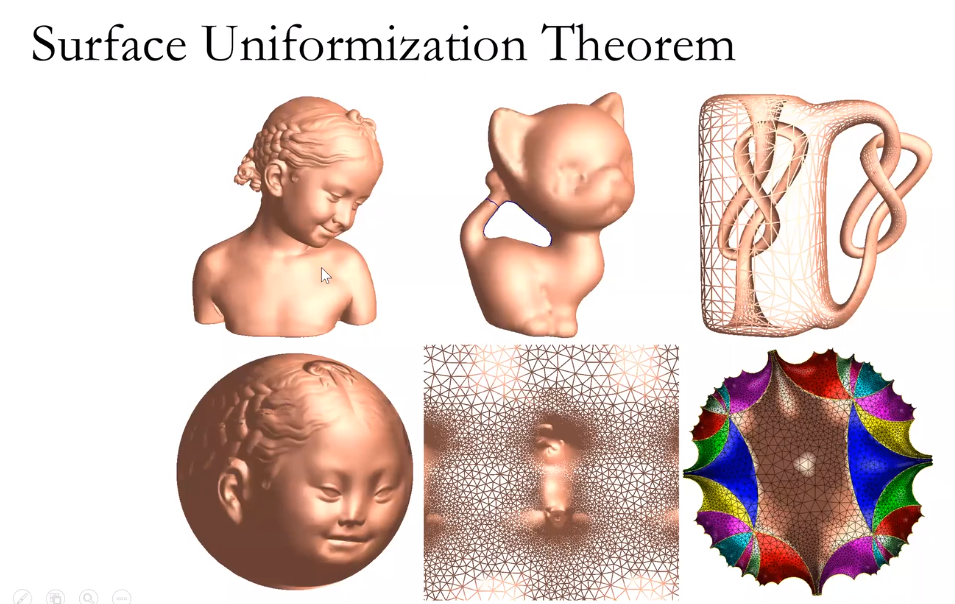
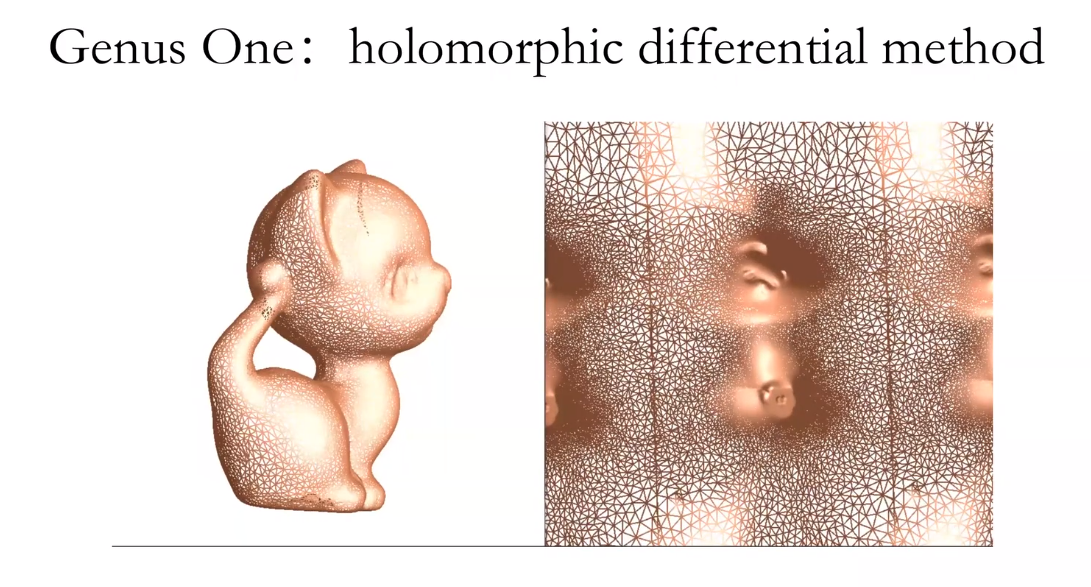
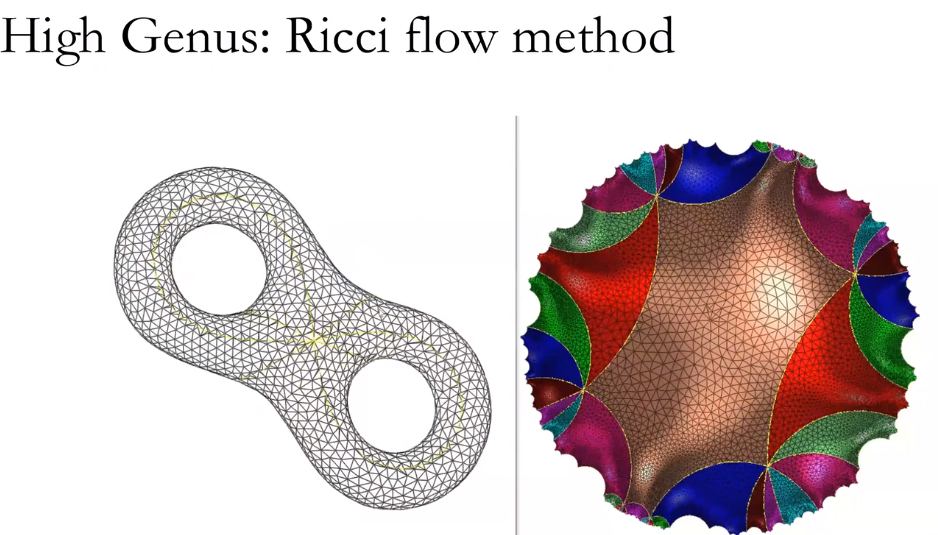
所有带度量的封闭曲面都可以共形映射到三种标准空间中的一种，球面，欧式平面或者双曲球面。
0亏格的封闭曲面保角变换到球面上。
亏格为一的曲面映射到欧式平面上。
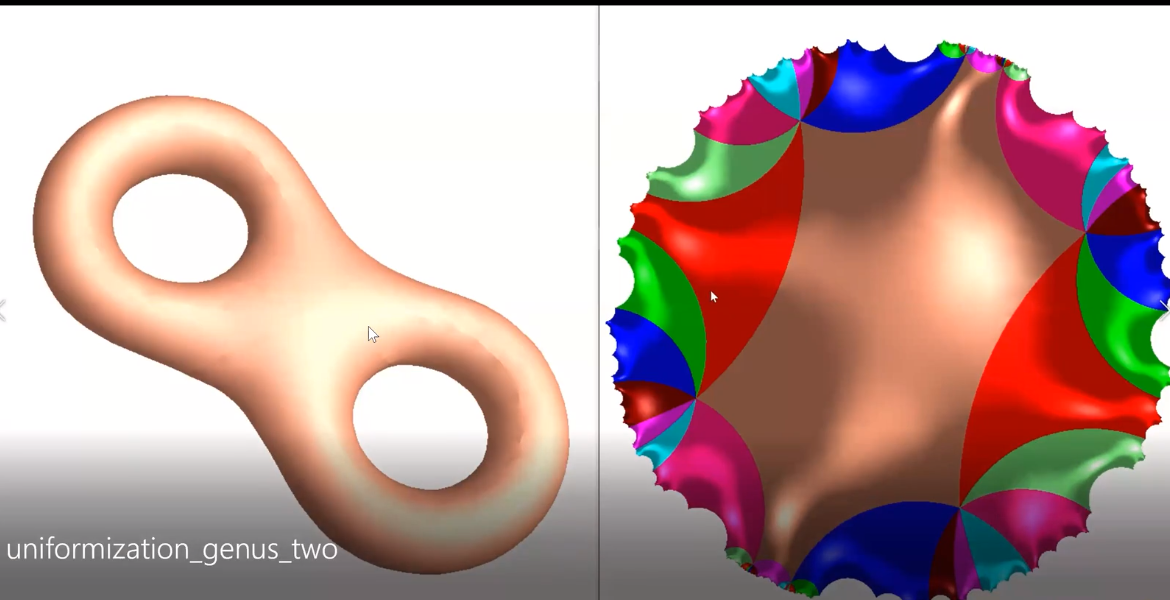
亏格为2的曲面覆盖整个双曲曲面。
带有边界的曲面。
1.调和映射（适用于亏格为0的曲面
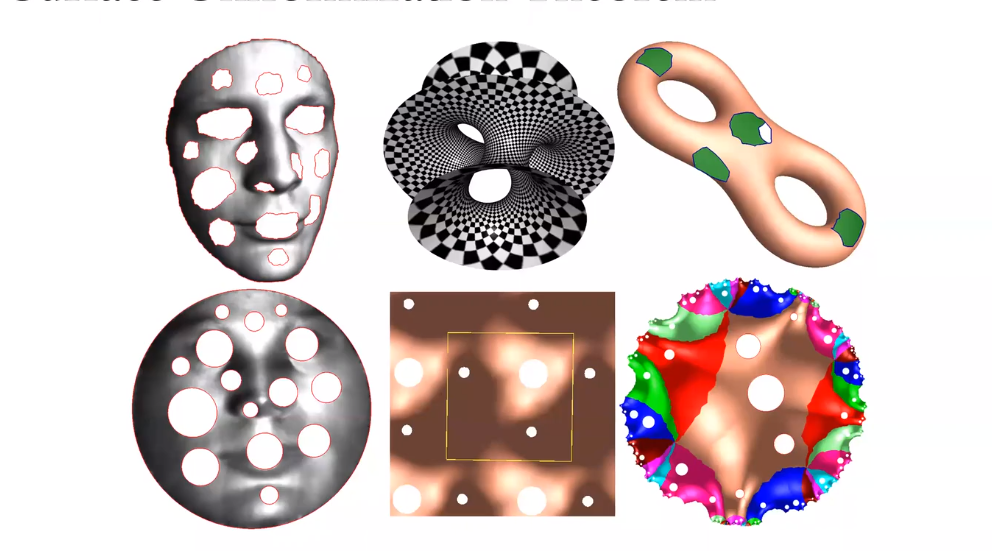
2.全纯微分（适用于亏格为1的曲面
找到散度和梯度为0的像静电场形式的，其映射具有唯一性。
3.Ricci 流（适用于高亏格曲面）
表面纹理映射参数化
传统纹理工艺浪费大量的内存
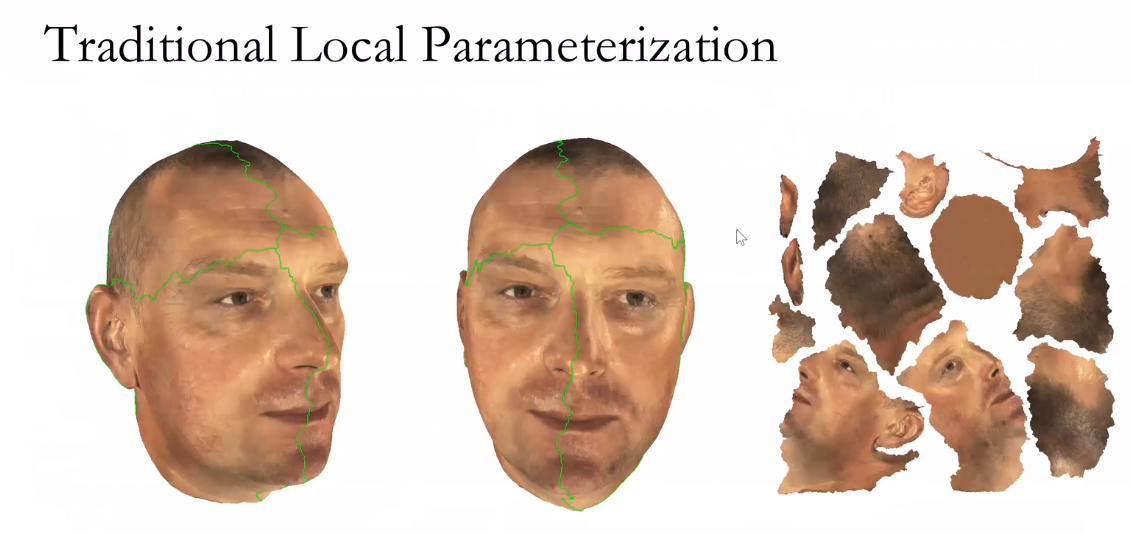
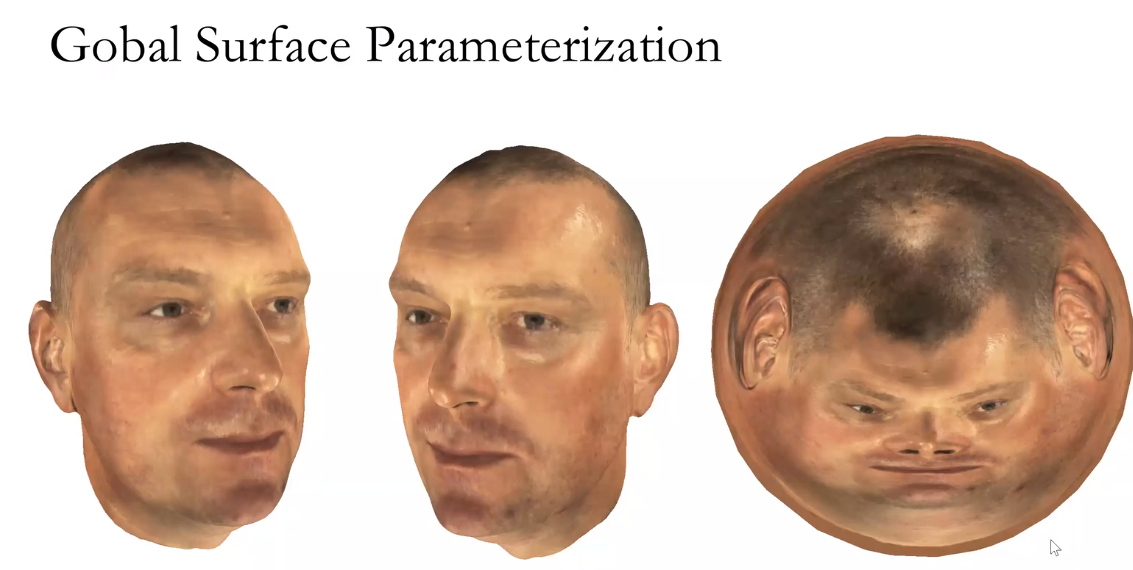
法向映射
保持角度和保持面积的到不同的映射
几何图像
使用2维图像保存3维模型数据。
如何处理大量的三维数据
使用三维技术，人们可以非常容易地得到三维的数据结构。
例如使用结构光的方法进行扫描，扫描速度非常快，解析度也高。
动态的表情变化每一帧有差不多50万个采样点。这样可以得到非常迅速的、大规模的三维数据的采集。
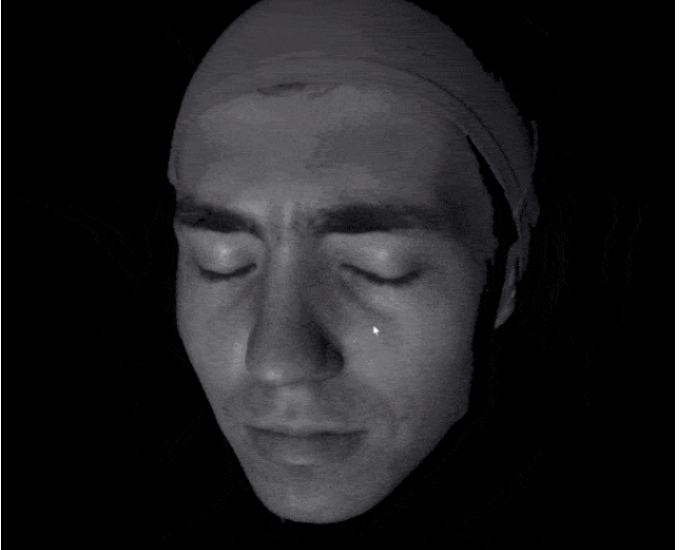
我们瞬间可以得到大量的三维数据，但是如何来处理这些非常难以处理的三维的数据？
平直空间的问题可以使用线性代数，而对于曲面的话无能为力，因此必须要引入现代的微分几何和共形几何。
角度不变，尺寸发生改变。
共形几何应用
人脸曲面配准
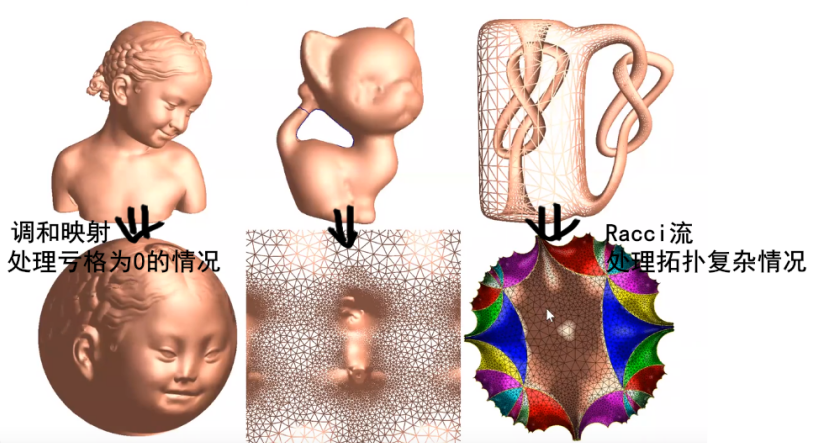
给定两张三维人脸，如何在他们之间，建立比较好的一一映射？我们的方法就是把三维人脸，用黎曼映照，映到二维的圆盘上。这样通过降维攻击，就把这三维问题变成了二维问题。二维问题，会简化非常多。
把这个男孩的这张脸映到女孩这张脸。第一步，用一些机器学习的方法，找到人脸上的特征点，比如眼角、鼻窝还有鼻尖，然后使特征点对齐。第二步，使得整个的畸变达到最小。使畸变最小这个映射，被称为泰希米勒映射。（?
畸变由什么决定呢？是由两族Foliation（叶状结构）决定，调和叶状结构决定。（？
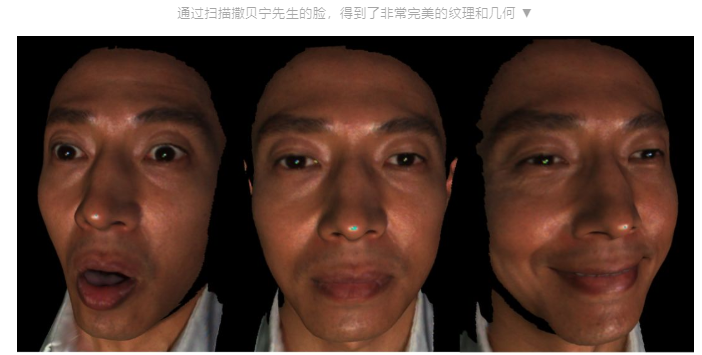
为什么要得到非常精细的映射呢？主要是为了做精准医疗。欧美的白人他们祖先生活在寒带，所以他的基因中缺乏抵御紫外线的功能。所以对于白人来讲，非常容易得皮肤癌，也就是所谓的黑色素瘤。黑色素瘤非常小，肉眼几乎不可见，低于毫米。如果用人工去筛查这个黑色素瘤就会非常痛苦。我们就发明这种方法，同一个人每隔一年扫描一次，然后精细地筛查在皮肤上逐点比较看哪一点皮肤发生突变。这样可以非常自动地找到这个黑色素瘤。所以计算机视觉在医学上也有很深的应用。
三维映射
动画与电影
动作捕捉和表情捕捉
动漫领域，这些方法也有很好的应用。在动漫电影中，动作捕捉和表情捕捉是非常关键的技术。比如武打片的动作捕捉，就是要得到各个关节的信息。但是动作捕捉非常容易，因为人的关节只有几十个，表情捕捉却非常难，表情的自由度有无穷多个。所以现在整个动漫产业，最困难的就是表情捕捉。那么怎么进行表情捕捉呢？
把动态的三维人脸，通过黎曼映照映到二维的圆盘上，然后用刚才的方法可以建立帧与帧之间的一一映射。
哦。也就是说在工程上这些数据的数据量压缩到最小同时保留了角度信息，可以还原。
表情移植到卡通人物上
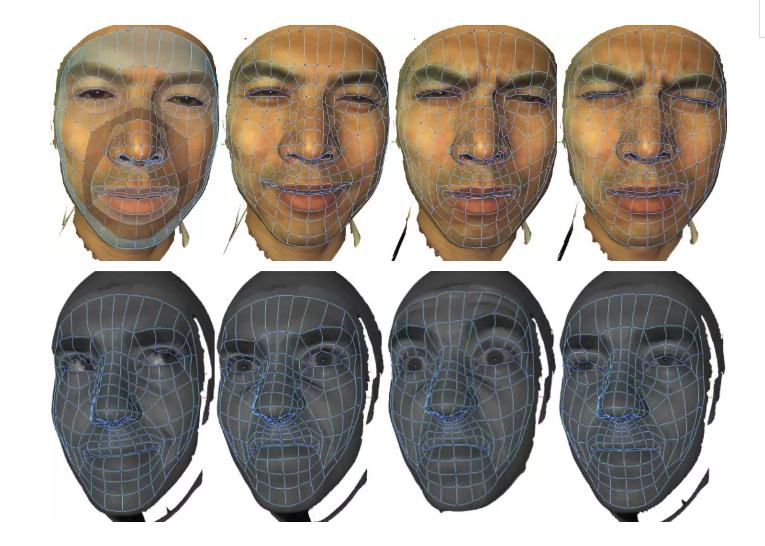
把一张蓝色的四边形网格贴到第一张脸上，依随这个人脸的变化而变化。这个蓝色网格上每一个点会得到三维空间中的一条轨迹，这个轨迹就代表了这个表情的信息。我们可以把这表情信息拿出来，去移植到其他的卡通人物身上。
虚拟演员
把三维的人脸表情拿下来，然后进行表情捕捉。建立一个虚拟演员。
现在明星拍摄非常非常昂贵。那么我们是不是可以把他的所有的表情以三维的方式记录下来，然后导演来决定，到哪一个情节、哪一个台词，用什么表情，从数据库中给它取出来。如果这样，我们不需要这个演员真正来出演，只需要得到他的数字版权就可以。
在这边找了一个演员，把他的一些标准表情给数字化，然后做了下面一个非常小的一个电影片段。这边的整个场景是假的，是用Maya（三维动画）做的。人也是假的，表情也是假的。所以我们相信虚拟演员这个技术，未来可以在VR、AR中很大地普及。
数据压缩
在VR,AR中，数据压缩是一个非常关键的问题。比如我们为了表达一张老人的脸，饱经沧桑、满布皱纹，需要大量的几何信息。如果要通过无线网络来传递这个信息，或者是本身硬件性能比较差，渲染速度就非常慢。如何来压缩这个复杂的几何信息是一个非常关键的问题。我们把一个老人头映到平面的圆盘，然后再控制每个区域在平面上的大小。比如说它曲率比较高的地方，皱纹比较高的地方，让它在平面的区域变得比较大。
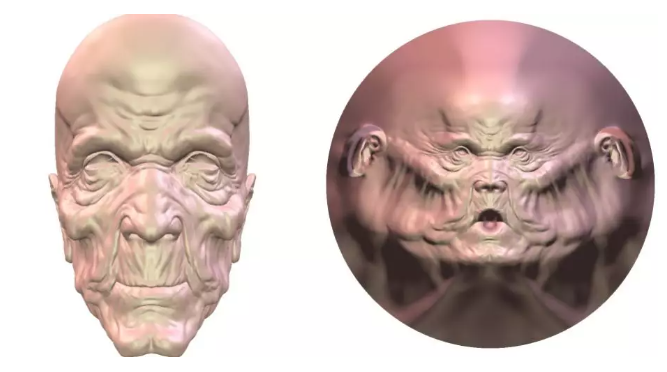
比如这幅图，我们在平面上采样，采样之后在平面上重新进行三角剖分得到这个简化的模型。这边如果我们只用2000个这个采样点，得到的是左侧这张人脸。如果用4000的话得到右侧这张人脸。所以增加采样率，可以使得图像几何的特征越来越细腻。这样就可以求得一个渲染的质量和这个所谓的空间的存储一个很好的一个平衡。这是在VR、AR中几何压缩的一个应用。
医学图像领域
脑图
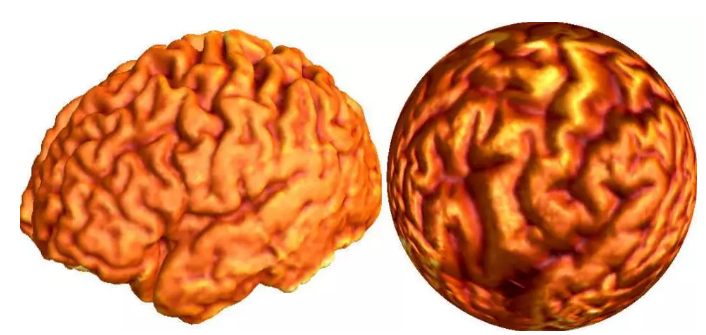
在医学图像领域，共形几何用得也非常广泛，比如说共形脑图。人的大脑，形状非常地复杂，有很多沟回，这些沟回，随着岁月的增长是会发生变化的。比较两个大脑本身来讲非常困难。通过刚才大一统定理，我们知道存在一个共形变换。把大脑映到单位球面上，并且这个映射，基本是唯一的。得到这个映射之后，我们为大脑的每一点，确定唯一的经纬坐标。这样可以在大脑上精确地定位，进行比较。
老年痴呆
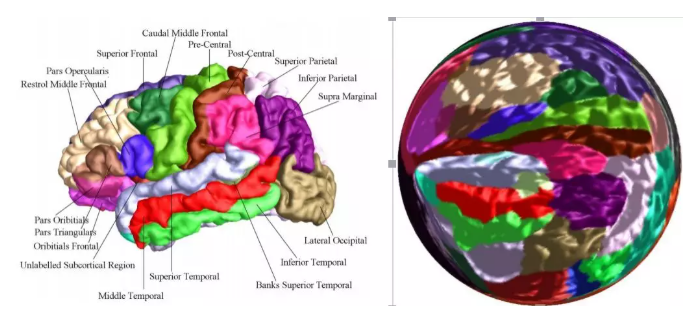
老年痴呆症是一个非常普遍的一个疾病。人的大脑根据功能有很多种分区。比如最中间的这个山谷，是胚胎期最先形成的一个皱褶，人的感情，基本存在这个皱褶两边。
下图中，不同颜色代表不同的功能区域。有的区域主管语言，有的区域主管着运动，有的区域主管感情，有的区域主管推理。老年痴呆，是对应的某些功能区域会发生萎缩。
如果我们通过共形脑图，来进行精确的比较，发现老人的语言中枢开始萎缩，可以让他学一门新的外语，这样就可以延缓他老年痴呆症状。如果他的感情中枢开始萎缩，让他多参加社交，如果他的运动中枢开始萎缩，让他去跳广场舞，这样可以加强对这个区域刺激。
癌症检测与虚拟肠镜
在医学图像中的，另外的应用，是关于癌症检测。直肠癌，是男子的第四号杀手，普通男子过了中年之后，肠子里面会长出一些息肉。如果息肉的位置长得不对，经常地摩擦溃疡，摩擦溃疡之后复合，复合之后又反复摩擦溃疡，它的DNA复制次数就会非常多，这样就非常容易出错，出错之后就会形成癌变。
从一个息肉变到癌变，一般需要5到8年，如果在这期间，进行了肠镜检查，就可以非常有效地预防和防止。但是传统的肠镜检查非常痛苦，病人需要全身被麻醉，同时肠镜检查的方式具有非常强的侵犯性。并且老年人的肠壁肌肉非常薄弱，很容易产生非常强烈的并发症。
还有一个很大的问题，直肠有很多皱褶，如果我们的息肉长在皱褶里面的话，传统的光学方法是看不到的，所以用传统的检测方式来进行检查会有大概30%的漏检率。
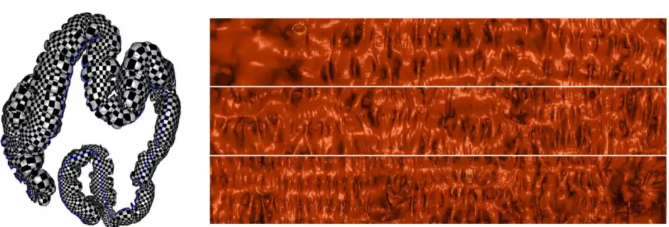
于是我们就发明了虚拟肠镜的方法，核心的想法就是–把肠子的皱褶打开摊平到整个平面上。如果以传统方式来检查，在活人身上是不可能实现的，但是用数字模型可以做到这一点。虚拟肠镜可以把所有肠壁的皱褶给摊开，把所有的息肉暴露出来，然后我们用CT来扫描人的直肠得到数字模型。于是，医生就可以戴上VR眼镜，来观察肠道的内壁。
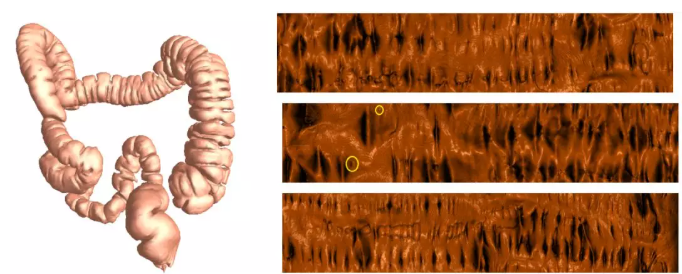
用伪彩色表达肠道内壁，那核心的话我们是要寻找一些肿瘤，或者一些比较大的息肉，那么在这个肠道中探索这个和真实的光学肠镜这个体验是非常相近的。通过这种方法我们就能看到一些比较可疑的息肉。
虚拟肠镜有非常多好处。第一，病人不需要全身麻醉。第二，医生和病人没有肢体接触，第三，我们能暴露所有潜在的息肉，提高诊断的准确率。
这个技术现在北美和日本用得非常普遍，在中国大陆，所有的医院几乎都有这套算法但是很可惜没有被真正用起来。那么它后边基于的是什么？非常艰深的几何用于医疗挽救了非常多的生命。
物联网路由器
交付保证贪婪路由，
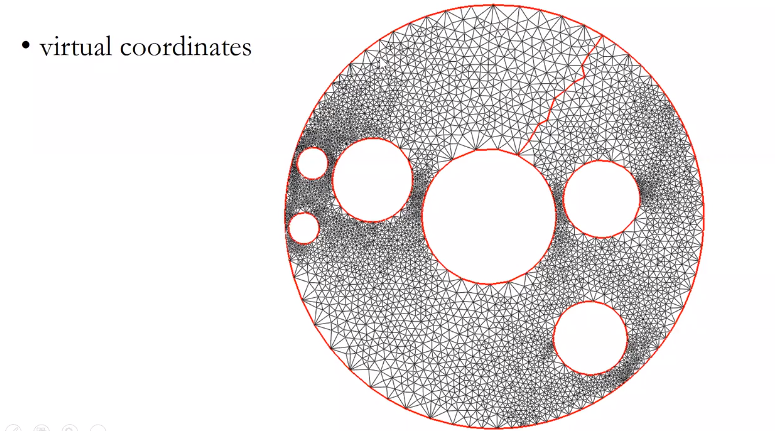
给传感器分配虚拟坐标
整形图像分析
比较微整容前后的差异
工业界
样条曲面要求2阶可导
四边形网格曲面
模拟仿真需要计算高质量的四边形网格，如何生成高质量的网格。
雕塑与力学结构
Reference:
几何为万物赋能——建筑、医疗、动漫、游戏…… | 凤凰卫视世纪大讲堂
Lecture 0 - Introduction to Computational Conformal Geometry
三维重建学习-1
想养成个习惯，学什么东西，比如深度学习什么的类别，在知乎上搜搜有没有前人的学习路线，在google,baidu上搜索看有没有书，在Youtube上搜搜有没有教程和介绍，在Coursera和Mooc，bilibili上看看有没有相关的课，youtube用英文搜索，在github上看看有没有相关开源框架，在淘宝上搜搜有没有相关的课程和书之类的，大致就是这几个方面。
1.图像处理基础概论
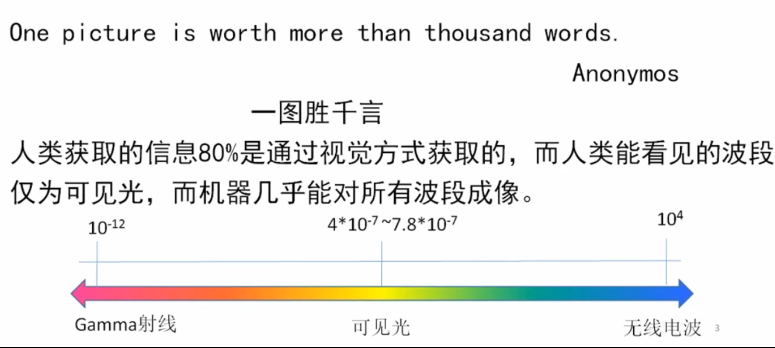
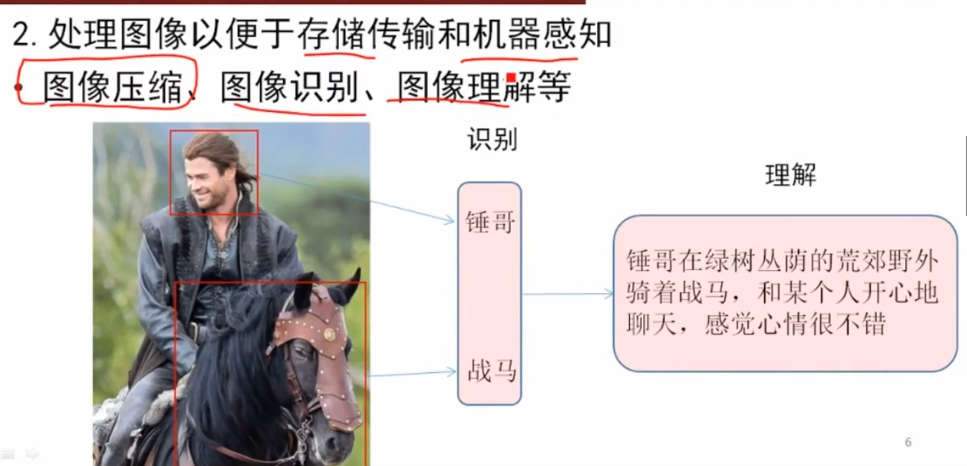
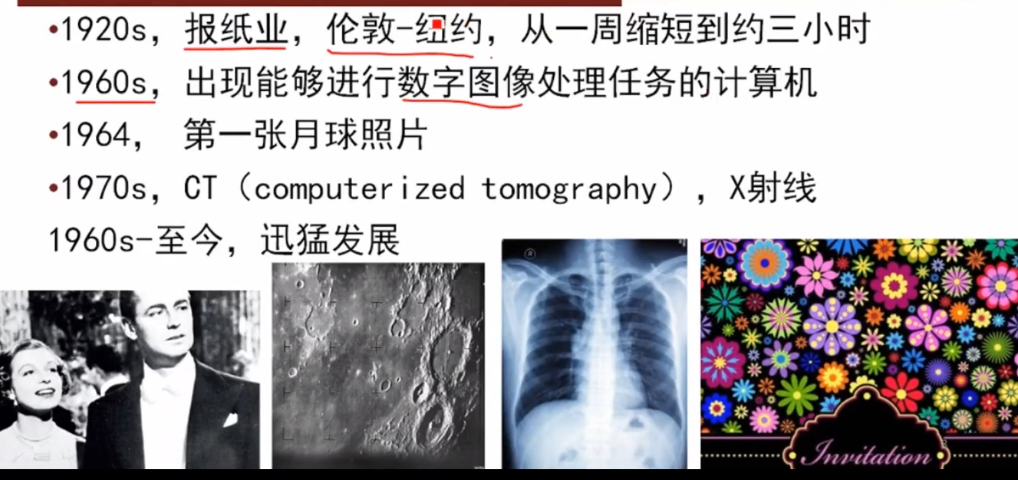
计算机的图像识别能力比人眼范围多
人眼的识别能力受主观限制，但是人眼对图像的理解能力很强
1.1图像处理的目的
1.2 图像处理简史
1.3 图像处理应用
1.4 图像处理内容
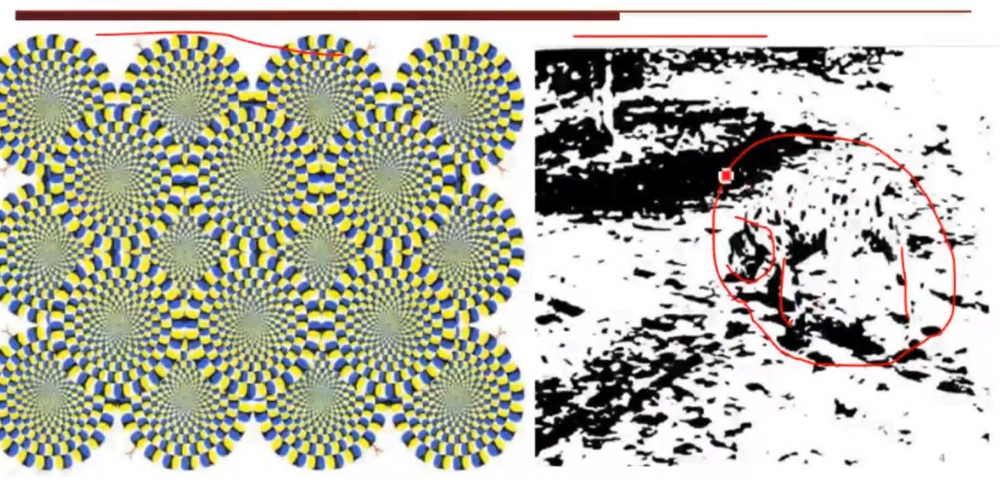
图像增强：直观理解应该是马赛克模糊和美颜什么的
1.5 图像处理构成
2.图像处理概念
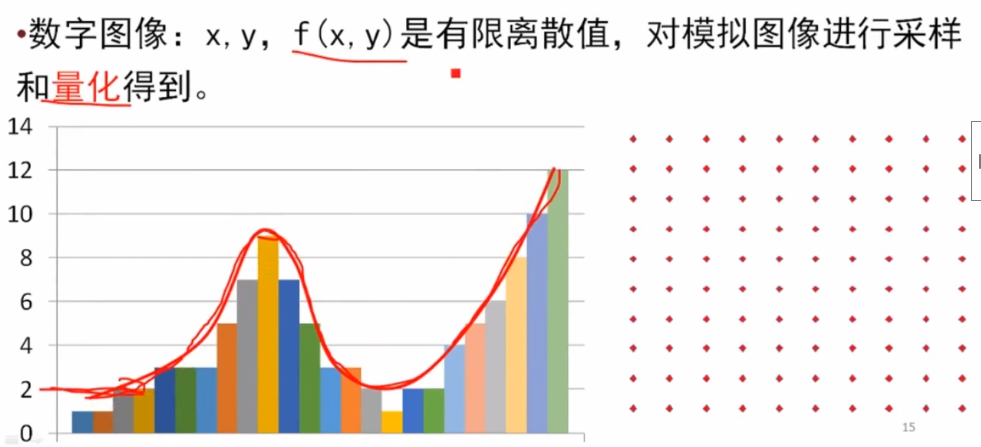
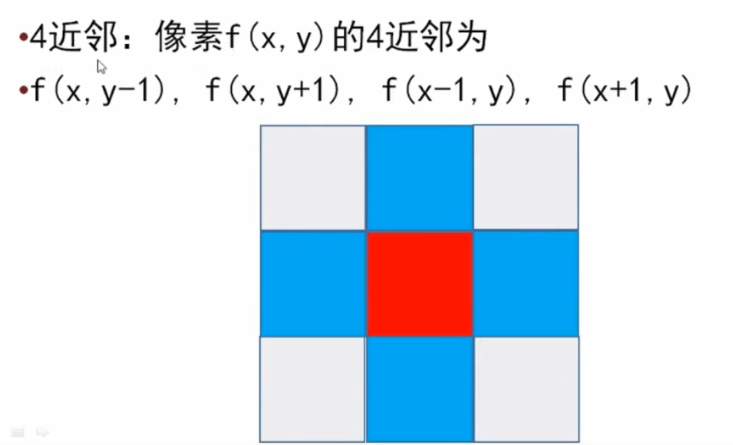
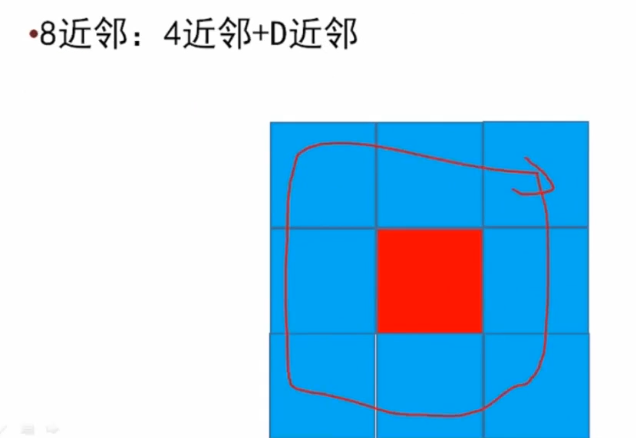
坐标和幅值，图像的概念
数字图像
灰度图像，彩色图像，二值图像
。。。这也太。不行学过画画想笑。。
采样
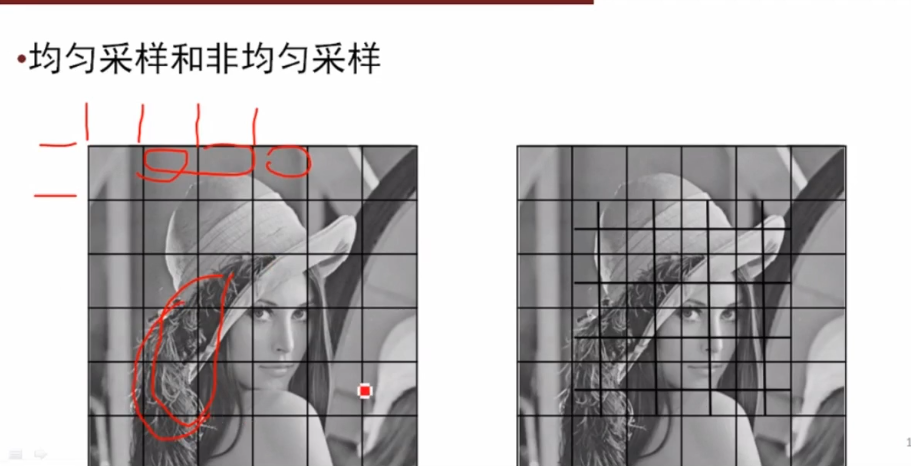
采样有点像绘画里的最小笔触。。
采样对图像的影响
缩小的时候要取的像素颜色值，近邻的颜色值
量化对图像的影响，灰度的级别
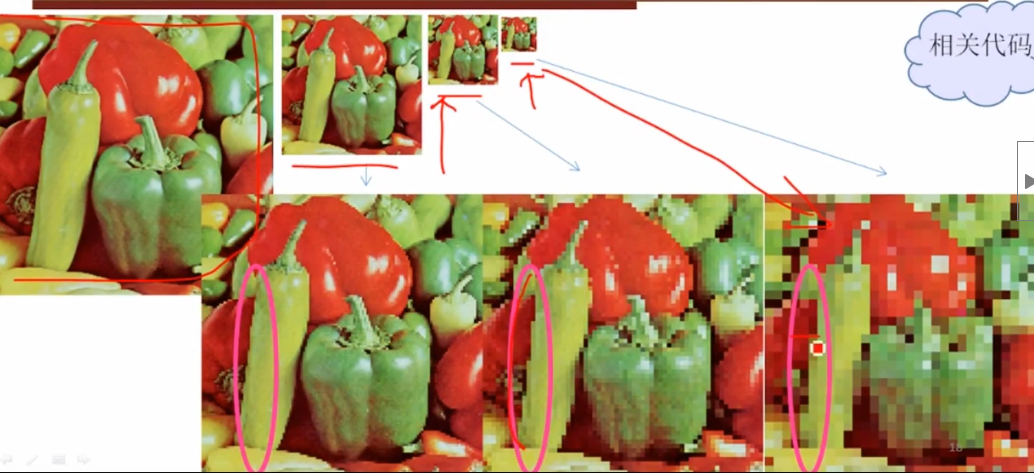
细节量
影响图像质量的因素
层次（灰度？
对比度
亮度(明度)
尺寸
细节(像素大小)
饱和度
像素之间的关系
4近邻
8近邻
连通
灰度值相等或者差值在某个范围内
通路
距离
图形学科研之路-1.开篇.Interactive computer graphics
知乎的书单，开始读了。【书单】图形学科研之路（持续更新）
genlib找的第一本书 Interactive computer graphics : a top-down approach with shader-based OpenGL / Edward Angel et
OpenGl这东西也用一些，网上很多教程也烂大街了，但是说实话到最后都没看下去，都是停在前面那点知识，这本书中一句话让我对API消解了纠结，确实学API的同时也了解了底层的算法实现。
1 | A graphics class teaches far more than the use ofa particular API, but a good API makes it easier to teach key graphics topics, including three-dimensional graphics, lighting and shading, client–server graphics, modeling, and implementation algorithms. We believe that OpenGL’s extensive capabilities and well-defined architecture lead to a stronger foundation for teaching both theoretical and practical aspects of the field and for teaching advanced concepts, including texture mapping, compositing, and programmable shaders. |
关于这本书的作者，看来看去我算是明白了，做图形学的就那么几批人。
Edward Angel 主页上没什么可看的，我简称这人叫爱吉，有用的信息就是他研究的领域volume visualization, virtual reality, and masssively parallel computing.，体积视觉化，虚拟现实，大规模并行计算。
He has taught over 100 professional short courses including a MOOC with Coursera and at both SIGGRAPH and SIGGRAPH Asia.
这人貌似还在慕课MOOC，Coursera上有开课的，之后去看看，SIGGRAPH SIGGRAPH Asia.也有他的课。
1.一些概念
光栅，帧缓冲，分辨率
之前一直不知道光栅是什么意思，光栅化是个啥，看了看发现大概理解为像素的数组就行了，像素数组的名字是帧缓冲，写出来相当于FrameBuffer[Pixels]，帧缓冲中像素的数目叫分辨率，这不就是数组的大小吗。。。帧缓冲深度就是像素比特数，决定能用多少个颜色 ，1bit只有黑白两个颜色，8bits有256个颜色，HDR分配的比特位更多，传统帧缓冲用整数，现在有了浮点格式来存储颜色值。
在非常简单的系统中,帧缓存只存储屏幕上显示的像素的颜色值。在大多数系统中,帧缓存存储的信息要多得多,比如为了从三维数据生成图像需要使用深度信息。在这样的系统中,帧缓存包括许多缓存,其中有一个或多个用于存储要显示的像素颜色,称为颜色缓存(colorbuffer)。狭义来说可以把帧缓存和颜色缓存当做同义词使用。
从几何实体到帧缓存中像素的颜色和位置的转换称为光栅化( rasterization)或者扫描转换(scan conversion)
第一章一些课后问题与答案
1.8 为了以足够高的速度刷新显示器来避免闪烁,帧缓存的速度必须足够快。一个典型的工作站显示器的分辨率可以是1280 x 1024,如果每秒钟刷新72次,那么帧缓存的速度必须有多快?这指的是从帧缓存中读取一个像素可以用多长时间。如果刷新频率为60 Hz,分辨率为480 x640的隔行扫描显示器呢?
1 | 视帧缓存的深度而定,以帧缓存为深度为1为例,速度为,1024*1280*1*72b=11.25MB/s,即读取一个像素用时倒数分之1每秒。隔行扫描, 72变30. |
1.9 制作电影的胶片所具有的分辨率大约是2000 x3000这样的分辨率对于制作与电影画质相当的电视动画意味着什么?
1 | 每帧480*640像素的视频显示仅含有300K像素(普屏动画),而2000*3000像素的电影帧有6M像素,约多了18倍的显示时间,因此需要18倍的时间渲染 |
2.编程
不是从三角形开始好评(不是XD)
2.1 Sierpinski 镂垫（感觉是茶杯垫一样的东西
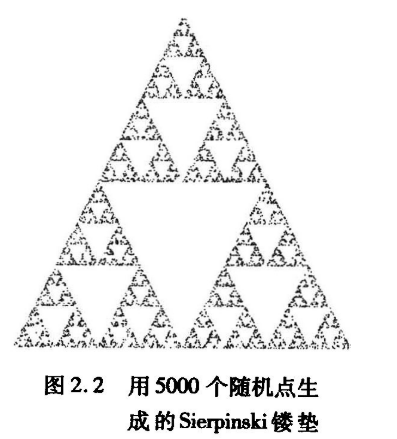
Sierpinski镂垫在分形几何领域中是重要的研究对象，可按递归和随机的方式来定义Sierpinski镂垫,当迭代的次数趋于无限时,其性质完全确定,并不随机,镂垫的三维版本与二维版本几乎相同。
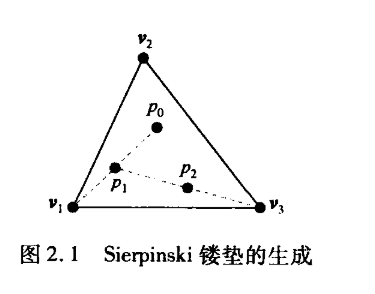
从空间中的三个点开始，只要这些点不是共线的,就定义了一个三角形也定义了一个平面。假定这个平面z=0,并且这些点在某个坐标系下的坐标是(x1,y1,0),(x2, y2, 0)和(x3, y3, 0).
构造过程如下:
1,在三角形内随机选择一个初始点p(x, y, 0)。
2,随机选择3个顶点之一。
3,找出p和随机选择的这个顶点之间的中点q。
4,在显示器上把这个中点q所对应的位置用某种标记(比如小圆圈)显示出来。
5·用这个中点q替换p
6.转步骤2
每当计算出一个新的点,就把它显示在输出设备上。这个过程如图所示,其中po是初始点,p,和p2是该算法首先生成的两个点。
2.2 具体编程有两种办法 立即绘制模式和延迟绘制模式
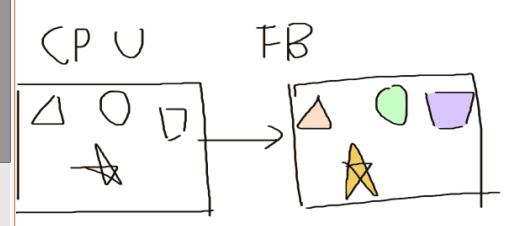
立即模式就是边算边显示，再显示的话就要重新计算。
延迟绘制模式是把所有的点计算出来，用空间换时间，把数据存储起来，不用重新计算，如果点的颜色发生变化，就可以重新发送而不需要重新计算。
2.3 两种模式的缺点
假定要制作一个动画,希望反复显示同一个对象,对象的几何外观不变,但是对象的位置可能要移动。每当对象在一个新的位置上显示,就需要把所有需要显示的点从CPU发送到GPU中。如果数据量非常大,那么从CPU到GPU的数据传输会成为显示处理的一个瓶颈。
解决方案:把顶点存储在GPU中，直接修改GPU中的数据。
如果以动画的形式显示这些数据,由于这些数据已经存储在GPU中,所以重新显示这些数据不需要额外的数据传输开销,而只需要调用一个简单的函数就可以修改对象移动后的空间位置数据。
问题的核心：生成点和显示点
2.4 图形API函数的分类
1·图元函数2,属性函数3·观察函数4,变换函数5·输入函数 6·控制函数 7,查询函数
这7个任务是不管体系结构，不管API都要实现的共性功能。
1.图元函数
点，线，像素，文本，曲线，面啥的基本图形
OpenGL只直接支持非常有限的图元集,如点、线段和三角形,应用程序可以使用OpenGL支持的图元通过逼近的方式来支持其他图元。对于许多OpenCL不支持的重要对象,例如规则的多面体、二次曲线、Bezier曲线和Bezier曲面,可以使用相关的库来支持。可以通过可编程着色器来高效地支持这些扩展的图元集。
2.属性函数
线的颜色，文本的字体等