く__,.ヘヽ.　　　　/　,ー､ 〉
　　　　　＼ ', !-─‐-i　/　/´
　　　 　 ／｀ｰ'　　　 L/／｀ヽ､           
　　 　 /　 ／,　 /|　 ,　 ,　　　 ',                                 
　　　ｲ 　/ /-‐/　ｉ　L_ ﾊ ヽ!　 i                   
　　　 ﾚ ﾍ 7ｲ｀ﾄ　 ﾚ'ｧ-ﾄ､!ハ|　 |  
　　　　 !,/7 '0'　　 ´0iソ| 　 |　　　
　　　　 |.从"　　_　　 ,,,, / |./ 　 |           
　　　　 ﾚ'| i＞.､,,__　_,.イ / 　.i 　|                   
　　　　　 ﾚ'| | / k_７_/ﾚ'ヽ,　ﾊ.　|           
　　　　　　 | |/i 〈|/　 i　,.ﾍ |　i　| 
　　　　　　.|/ /　ｉ： 　 ﾍ!　　＼　|          
　　　 　 　 kヽ>､ﾊ 　 _,.ﾍ､ 　 /､!           
　　　　　　 !'〈//｀Ｔ´', ＼ ｀'7'ｰr'          
　　　　　　 ﾚ'ヽL__|___i,___,ンﾚ|ノ
　　　　　 　　　ﾄ-,/　|___./
　　　　　 　　　'ｰ'　　!_,.:

(1) 回顾你过去将近3年的学习经历

当初你报考的时候，是真正喜欢计算机这个专业吗？

并非如此，当时只是对其他的专业无感，没有太多的兴趣。

你现在后悔选择了这个专业吗？

并不后悔，当初填报志愿的时候选择了很多专业，最后觉得还是计算机比较适合，感觉几年前的自己对专业的理解太过狭隘，如今找到了自己想努力的方向还是非常开心的。

你认为你现在最喜欢的领域是什么（可以是计算机的也可以是其它领域）？

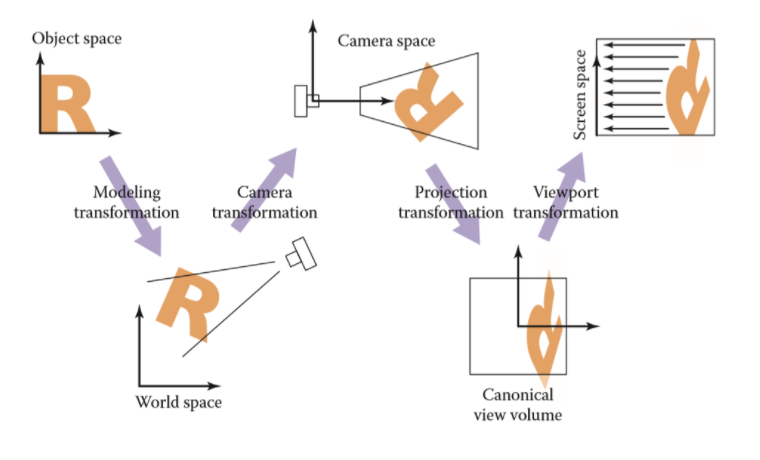
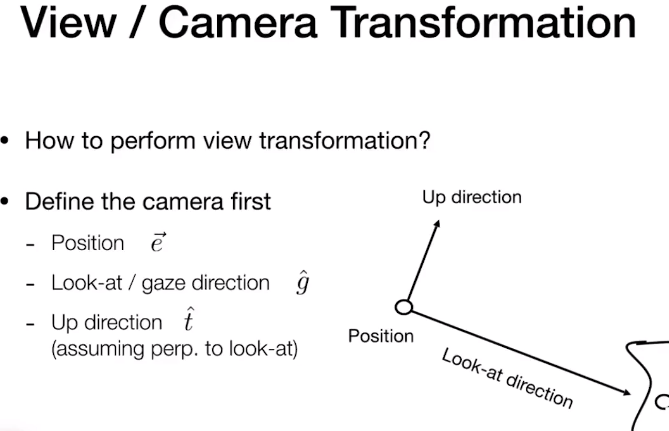
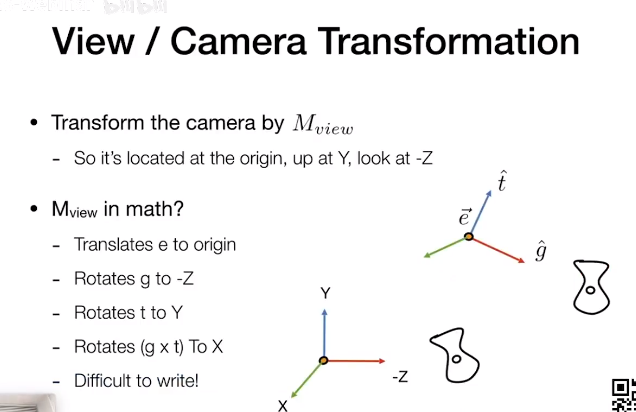
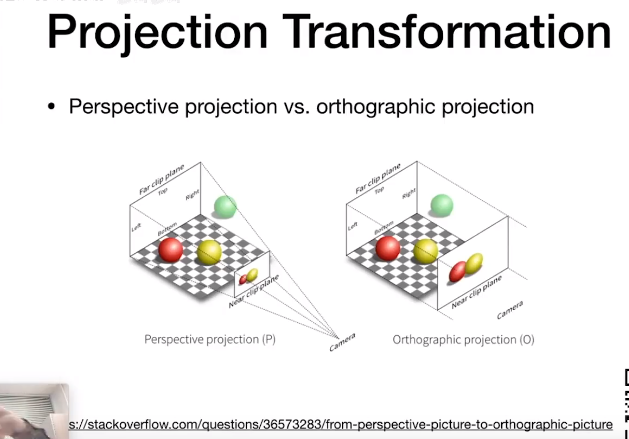
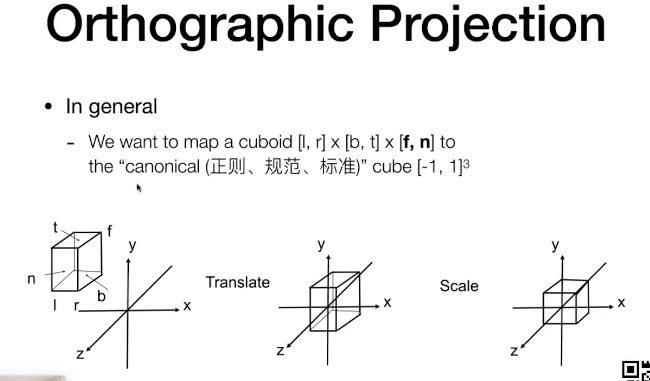
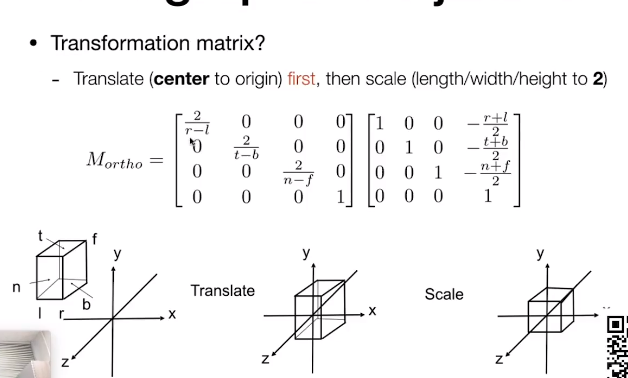
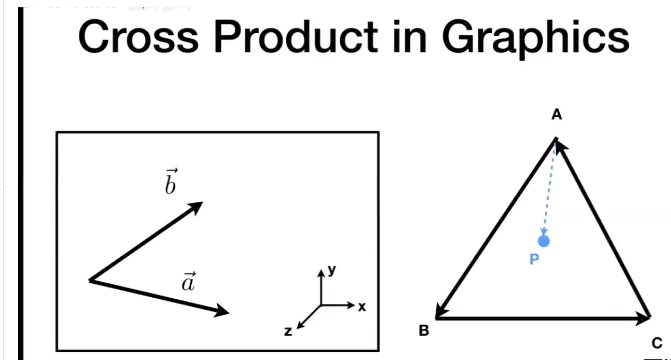
计算机图形学与3D技术，爱好绘画，热爱动漫文化。

(2) 总结你现在已经掌握的知识

你都具备了那些专业知识和能力？

分析小问题和解决小问题，阅读文档，搜索资料，越是深入越觉得知识深似海底，自己不过是窥见了冰山一角，还有很多知识需要学习，列如UE4,Blender等3维软件的一些文档我如今还没看完。

你认为你已经为成为一个合格的计算机软件工程是做好准备了吗？

严格来说，思想准备倒是一直有，只不过目前深感技术和知识上的欠缺需要时间去弥补

在专业技术、个人能力以及其它方面你还有那些欠缺？

目前主要是阅读书籍和文档以及源代码，专业技术可能学的不太系统，打算之后有时间重新来一次，个人能力的话…我想想,欠缺的很多啊…

(3) 畅想未来

对照材料中前人的经历，你还准备从事计算机这个行业吗？

未来的事情谁都说不定，但是目前是这样打算的。

你认为与其它专业的同学相比，你的优势都有哪些？

个人有个人努力的方向，朝着自己喜欢的方向前进就好了。

对已经不远的将来，你的职涯规划是什么？

有打算成为一名Computer Graphic Programmer。

自嘲一般

受光面的判断

老实讲，上色上手的第一个问题就是那里要画暗，哪里要画明。

强迫硬边

减少CPU消耗在边缘处理上(单核CPU,绘画经过练习可以成长为多核CPU)

覆盖图层的经验与控制力

第二个例子：K大谈日系平涂如何让光影更加真实

原因:初学者想做日系平涂但是又想要光影更加真实，因此猜光影导致明暗交界线混乱。

光影似对非对会影响画师日后的提升，一直处于半吊子的状态

改后

Version1

Version2

留下的疑问:第一层亮暗解决之后，如何画接下来的微妙的变化，接之前的厚涂篇，用弱对比塑造的手段画亮中暗和暗中亮。

总结:找参考

練習光影的第一步,在作畫之前,先找個真實參考來看,可以大幅降低純靠想像帶來的不確定性

先给出两个公式:厚涂公式和渐变公式

赛璐璐+弱对比=厚涂

渐变=弱对比面的衔接

赛璐璐

画师:米山舞

厚涂

画师:HJL

弱对比

按不科学的分类法，绘画似乎分为两个流派，分别是厚涂和赛璐璐，不过K在教导学生的时候明确指出厚涂就是赛璐璐。

K大的解释是 1.二分切出一个比较明显的光影块面（赛璐璐） 2.在明和暗中各自进行弱对比的塑造(厚涂) ，那么如果封印喷枪使用硬色块来画的话，其边缘就会变得全是硬边，画家就不需要去考虑哪里需要用涂抹笔进行涂抹，从结构上来说，渐变形成的原因是因为有足够多的弱对比面，就像球体一样光滑的面也可以简化为低多边形。

当然弱对比在k大的体系里算是塑造的一环，这就是后话了。

Blender 平直着色

Blender 平滑着色

Low Poly 低多边形

就如同Low Poly 低多边形的概念一样

在这种概念下 ，渐变就是小的凹凸起伏导致的明度的微弱变化

渐变

渐变=弱对比的块面衔接

总结

赛璐璐+弱对比=厚涂

渐变=弱对比面的衔接

Transformation 变换

rotation 旋转 反向动力学 IK

旋转矩阵

线性变化

Scaling 缩放

非均匀缩放

镜像

剪切矩阵

Translation 平移

齐次坐标 Why?

平移不是线性变换，我们不希望平移是一种特殊的变换

引入齐次坐标的cost是什么？

增加维度w 引入齐次坐标

向量具有平移不变性 What if you translate a vector?

《计算机图形学(OpenGL版)》的作者F.S. Hill Jr.曾说过一句话：

齐次坐标表示是计算机图形学的重要手段之一,它既能够用来明确区分向量和点,同时也更易用于进行仿射（线性）几何变换

于是我们知道，其重要性，主要有二，其一是区分向量和点，其二是易于进行仿射变化(Affine Transformation)

point+point = 齐次坐标系下 两点的中点

仿射变换

2D Transformation

S(Sx,Sy) R(α) T(tx,ty)

逆变换

组合变换

矩阵顺序：
$$
\begin{equation}
T_{(1,0)} \cdot R_{45} \cdot 矩阵
\end{equation}
$$

如果不以原点进行旋转呢？

对矩阵进行分解

$$
\begin{equation}
\mathbf{T}(\mathbf{c}) \cdot \mathbf{R}(\alpha) \cdot \mathbf{T}(-\mathbf{c})
\end{equation}
$$

3维变换

先线性变换->后平移 平移对形状影响不大 可以放在最后 也可以写在矩阵最后一列进行组合

Transformation Cont

旋转矩阵的逆等于其转置 正交矩阵

scale translation

rotarion matrix

任意方向的旋转 欧拉角

绕任意轴旋转 formula

$$
\begin{equation}
\mathbf{R}(\mathbf{n}, \alpha)=\cos (\alpha) \mathbf{I}+(1-\cos (\alpha)) \mathbf{n} \mathbf{n}^{T}+\sin (\alpha) \underbrace{\left(\begin{array}{ccc}
0 & -n_{z} & n_{y} \
n_{z} & 0 & -n_{x} \
-n_{y} & n_{x} & 0
\end{array}\right)}_{\mathbf{N}}
\end{equation}
$$

视图变换

modeling tranformation 模型变换

将虚拟世界中或者更具体点，游戏场景中的物体调整至他们应该在的位置

View Camera tran. 相机变换

MVP 三变换 得到物体与摄像机的相对位置

摄像机变换的目的是得到所有可视物体与摄像机的相对位置，把物体和摄像机一起做移动，如果能够把摄像机的坐标轴(假设为u,v,w 分别对应原世界空间中的x,y,z)移动到标准的x，y，z轴，那么此时物体的坐标自然是相对坐标。

因此核心问题就变成了如何表示或者说如何将camera的坐标系与原世界坐标系重合

定义3个东西

• 相机或眼睛位置 (eye postion) e
• 观察方向 (gaze postion) g
• 视点正上方向 (view-up vector ) t

相机的三个属性

其中u，v，w分别对应标准坐标系下的x，y，z，示意图如下：

不直接拿 t 当做基底向量是因为摄像机的头可能是歪着看的

约定相机永远看向-Z方向，约定标准位置

把相机的uvw移到xyz标准坐标去，朝向为-z轴

平移矩阵 平移相机位置到原点上去 和旋转矩阵

原始的旋转 从相机到世界原点的矩阵不好的到，反过来求其逆，把坐标原点旋转到相机，求逆就是其转置，因为旋转矩阵是

正交矩阵，就如同在blender里按下0到相机的视角。

Projection tran. 投影变换

正交投影Orthographic projection 和透视投影 Perspective projectivre

锥与正方体的区别,坐标标准化，正交投影直接把z坐标给扔掉就是正交投影的视图

正交投影

[left.right] [button,top] []

矩阵平移缩放标准化

透视投影

齐次坐标的缩放不变性

远平面到近平面的矩阵变换，从侧视图想起

一句逻辑推出x和y的解答 z的部分设为未知

推理出来矩阵的第1，2，4行只剩第3行的值

z用n代替 矩阵第三行乘原点得到n^2,但是A,B可能等于0，只有这一个条件还不行

使用原平面的中心点得到第二个约束条件

解的透视投影矩阵

作业0:

1.添加->正方体

2.面->交集(切割)

3.网格->分离->按松散块

前言（Introduce）

Krenz是我很喜欢的画师，其主要在台湾从事绘画教育活动，也是我绘画入门的老师，逻辑思维严谨，我个人觉得这和k大的性格和还有工学经历有关，其讲课的方式浅显易懂，容易让学生所接受，K大的课总是喜欢用类比的方法让一些比较难的概念变得浅显易懂，其价格也比较便宜实惠，和一些乱七八糟的教学相比拥有很高的性价比，其三门课循序渐进，让不会绘画，从零开始的初学者有了一个比较好的入手点，因为看了看K大的课件在电脑里堆得时间实在太长，因此想趁此机会做一下总结。

我个人并非专业画师，只是基于业余爱好的经验来写这些东西，其中大部分总结也是看了k大课件里的部分总结来的，如果专业人士看了之后觉得哪里理解有误或者不妥的地方还请不吝指出。

笔者所说的话可能不是特别正确，因为我个人也是一个嘴上的巨人，绘画群和老师经常称没画就一大堆问题的人叫嘴上的巨人，用嘴画画等等，因为绘画的主观性，导致所有观众都能插一嘴，也不像数学那样有门槛，因此请各位问老师问题的时候带着自己的画，这样一方面老师可以看出画中的错误对症下药，一方面不会因为理解有偏差导致隔空抓药。绘画一方面是实力的问题，另一方面你也得画啊() ，所以不要全相信我总结的东西。

第一章:主角(焦点Focus)

一般来讲，绘画的画面所表示的必有一个(至少有一个)主题或者主角，就像写小说一样，要让别人(观众)的视线往主角看，那么画家面对一张白纸的时候就要考虑主角在白纸的哪个位置，之后的所有表现手法都是为了表现主角服务的，一般来讲，我们把画面中观众第一眼看到的事物作为主角，就如同刀剑神域动画开始的时候也是从主角桐人开始的，而不是从别的角色开始，但是这一部分并非是浑然天成的，动画有剧本的安排让主角第一个出场，所有作品的角色，其出场顺序是经过可以安排的，绘画也是同理，小说家写作的时候要确定下这部小说的背景历史作为框架(十字线)，剧本有着主线任务和支线任务，明线(十字线和集中线)和暗线(点景)，正面描写，集中线太过直白，我们需要一个隐晦的表达来让集中线表达出来，但又不让观众察觉出来，集中这个概念不一定要用直线。甚至不一定必须用线，使用几何图形暗示也可以。

知道了这个概念就让我们看下面几幅画。

看一下这个空白的长方形框，如果你不是闲的蛋疼，一般来讲不会多看它一眼，因为画面里什么都没有。

试试放个点进去，我们的注意力会移动到右上角。

再加个比他大的点进去，这回我们不会先看右上角,而会先看左下角之后才会注意到右上角，这个新来者(Focus2)胜过了前者(Focus1)，成了画面新的焦点(Focus)。

再画一个比较大的点(Focus3)，你的眼睛会首先看更大的点，然后移动到第二大的点(Focus2)，紧接着是第三大的点(Focus1)。依据这个原理，画师可以四处移动他们的焦点，让你在画面中绕啊绕，就像在画面中旅行一样。

焦点非点

在一幅画中，任意一个眼神聚集的地方叫做“焦点”。每幅画都有一个或者多个焦点，或分散或集中，它们不一定是字面意义上的点，也可以是线条(图6)、二维的形状(图7)，或者是三维的立体结构(图8)，图8和图9中的“团”焦点是由暗色和淡色阶所表示的,当然它们也可以是彩色的。正确地处理这些焦点,不论是将其单独呈现还是合并使用,都会在创作优秀画作时起到重要作用。

这是 XilmO@夕末(PixivID=19389056)的两幅画，我觉得不用我说明，我们一眼就能看出来焦点是女孩，同时我们的视线也会朝向焦点。

怎么说呢。。

这群漫画家真的是在那命换作品。

势

来自漫画镖人

系统重装要安装的软件:

驱动精灵 火绒 V2Ray-core 网易有道词典 向日葵

坚果云 百度网盘 MEGA 小米云服务 WPS office potplayer(网页)

typora 网易云音乐

Eagle Treesize free Steam blender Bandizip(类似的有Winrar)

QQ(网页或者TIM) 微信 腾讯文档 腾讯桌面整理Lite

NVIDIA GEForce Expericence everything

VisualStudio Git Nodejs Desktop Github Cmake-gui

bilibilijj IDM

Anaconda（Python） 论文-Zotero

主机额外安装:

炉石传说以及官方插件 战网 炉石传说盒子

Ubisoft Game Launcher Epic Game Launcher UE4

SAI2破解

替代品

下载器

IDE

办公软件

树莓派有关软件

绘画软件

3D软件

插件

学习教育

语言学习

旋转的例子

图形学中向量的默认形式是列向量

叉乘公式

$$
\vec{a} \times \vec{b}=\left(\begin{array}{l}
y_{a} z_{b}-y_{b} z_{a} \\
z_{a} x_{b}-x_{a} z_{b} \\
x_{a} y_{b}-y_{a} x_{b}
\end{array}\right)
$$

$$
\vec{a} \times \vec{b}=A^{*} b=\left(\begin{array}{ccc}
0 & -z_{a} & y_{a} \\
z_{a} & 0 & -x_{a} \\
-y_{a} & x_{a} & 0
\end{array}\right)\left(\begin{array}{l}
x_{b} \\
y_{b} \\
z_{b}
\end{array}\right)
$$

$$
\begin{array}{l}
\vec{x} \times \vec{y}=+\vec{z} \\
\vec{y} \times \vec{x}=-\vec{z} \\
\vec{y} \times \vec{z}=+\vec{x} \\
\vec{z} \times \vec{y}=-\vec{x} \quad \vec{a} \times(\vec{b}+\vec{c})=\vec{a} \times \vec{b}+\vec{a} \times \vec{c} \\
\vec{z} \times \vec{x}=+\vec{y} & \vec{a} \times(k \vec{b})=k(\vec{a} \times \vec{b}) \\
\vec{x} \times \vec{z}=-\vec{y}
\end{array}
$$
叉乘可以定义左右和形状的内外两侧信息，起到定向的作用

$$
\begin{array}{l}
\vec{a} \times \vec{b}=+\vec{z} \quad \quad a在b的左侧 \\
\vec{b} \times \vec{a}=-\vec{z} \quad \quad a在b的右侧\\
\vec{AB} \times \vec{AP}=+ \\
\vec{BC} \times \vec{BP}=+ \\
\vec{CA} \times \vec{CP}=+ \quad \quad 如P点在AC右侧,则\vec{CA} \times \vec{CP} 为负值 \\
如三角行逆时针,只要所有的叉乘值都为正值或都为负值就可判断在三角形内部，从而忽略给定的三角形的顺序 \\
在边上的情况被称为 corner case 这时候开发者自己说了算\
\\
\end{array}
$$

虚拟机安装问题

Not in a hypervisor partition (HVP=0) (VERR_NEM_NOT_AVAILABLE).

AMD-V is disabled in the BIOS (or by the host OS) (VERR_SVM_DISABLED).

解决方法

1.Windows设置 - 更新和安全 - 回复 - 立即重新启动

2.Troubleshoot -> Advanced option – > UEFI Firmware Settings -> Restart

3.在BIOS中找到Virtualization 选项，它常位于Advanced 或 System Configuration 选项卡下

4.设置Virtualization 的状态为Enabled。

AMD和Intel的设置不一样

Eigen库的使用问题

Eigen库的使用用例

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68

#include<cmath>

#include<iostream>

#include "../../Eigen/Core"
#include "../../Eigen/Dense"

int main()
{
    // Basic Example of cpp
    std::cout << "Example of cpp \n";
    float a = 1.0, b = 2.0;
    std::cout << a << std::endl;
    std::cout << a / b << std::endl;
    std::cout << std::sqrt(b) << std::endl;
    std::cout << std::acos(-1) << std::endl;
    std::cout << std::sin(30.0 / 180.0 * acos(-1)) << std::endl;

    // Example of vector
    std::cout << "Example of vector \n";
    // 向量定义
    Eigen::Vector3f v(1.0f, 2.0f, 3.0f);
    Eigen::Vector3f w(1.0f, 0.0f, 0.0f);
    // 向量输出
    std::cout << "Example of output \n";
    std::cout << v << std::endl;
    // 加法
    std::cout << "Example of add \n";
    std::cout << v + w << std::endl;
    // 点成
    std::cout << "Example of scalar multiply \n";
    std::cout << v * 3.0f << std::endl;
    std::cout << 2.0f * v << std::endl;

    // Example of matrix
    std::cout << "Example of matrix \n";
    // 矩阵定义
    Eigen::Matrix3f i, j;
    i << 1.0, 2.0, 3.0, 4.0, 5.0, 6.0, 7.0, 8.0, 9.0;
    j << 2.0, 3.0, 1.0, 4.0, 6.0, 5.0, 9.0, 7.0, 8.0;

    // 矩阵输出
    std::cout << "Example of output \n";
    std::cout << i  << std::endl;
    std::cout << j << std::endl;
	//矩阵加法
    std::cout << " matrix add matrix i + matrix j" << std::endl;
    std::cout << i+j << std::endl ;
    //矩阵点乘
    std::cout << " matrix scalar multiply i * 2.0" << std::endl;
    std::cout << i*2.0 << std::endl;

    //矩阵乘法
    std::cout << "matrix multiply i * j" << std::endl;
    std::cout << i * j << std::endl;

    std::cout << "matrix multiply vector i * v" << std::endl;
    std::cout << i * v << std::endl;
    std::cout << v.transpose()*i << std::endl;//reslut is different 
    //14
    //32
    //50

    //Transpose result is 30 36 42


    return 0;
}