Transformation 变换
rotation 旋转 反向动力学 IK

旋转矩阵

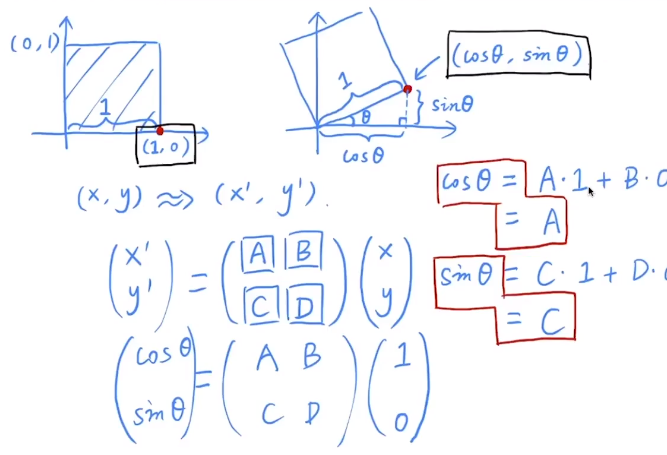
线性变化

Scaling 缩放

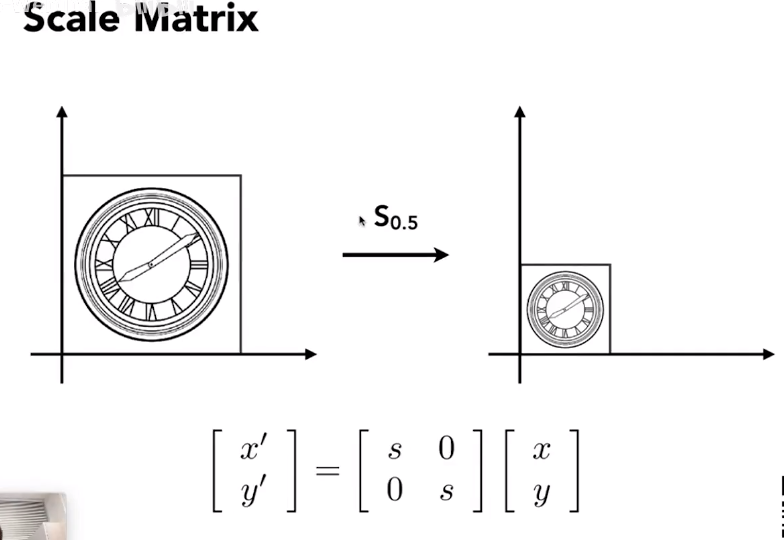
非均匀缩放

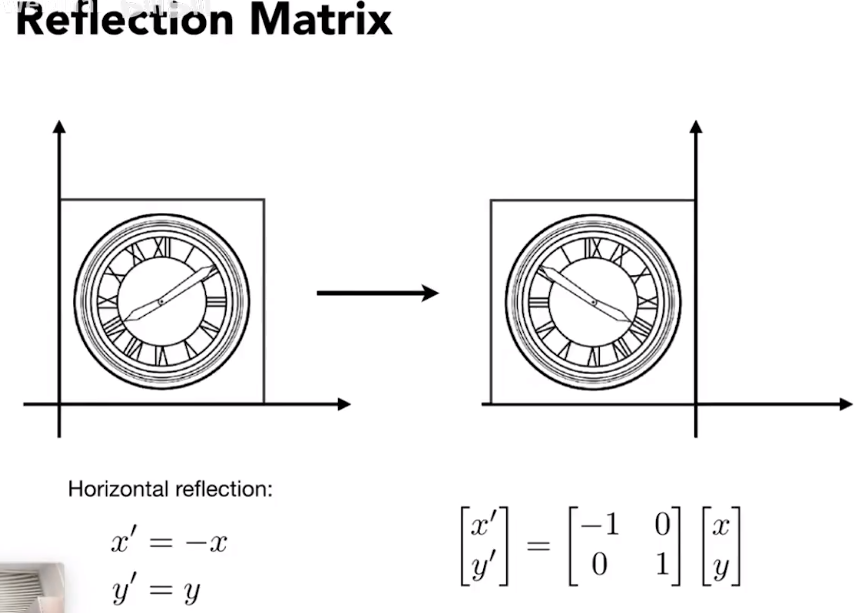
镜像
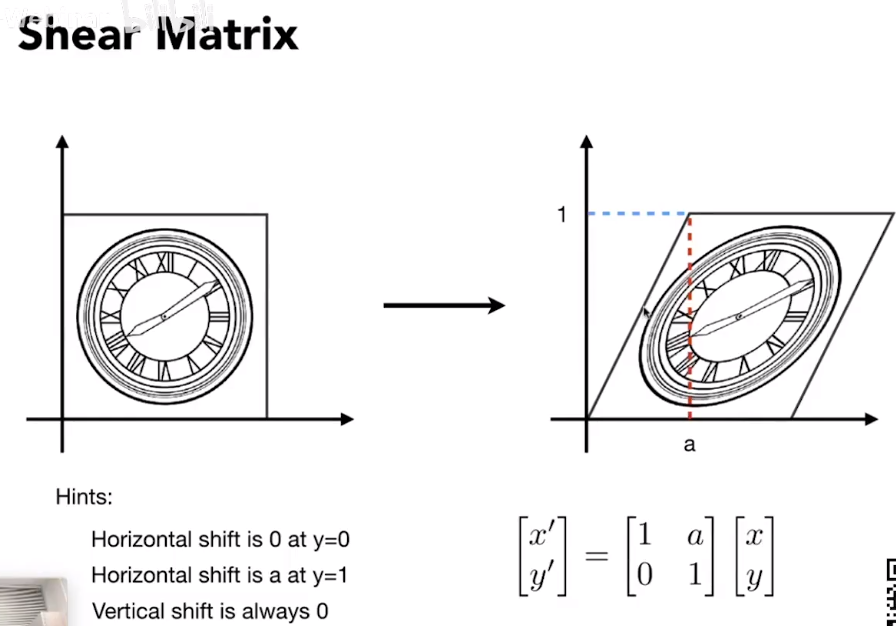
剪切矩阵
Translation 平移
齐次坐标 Why?
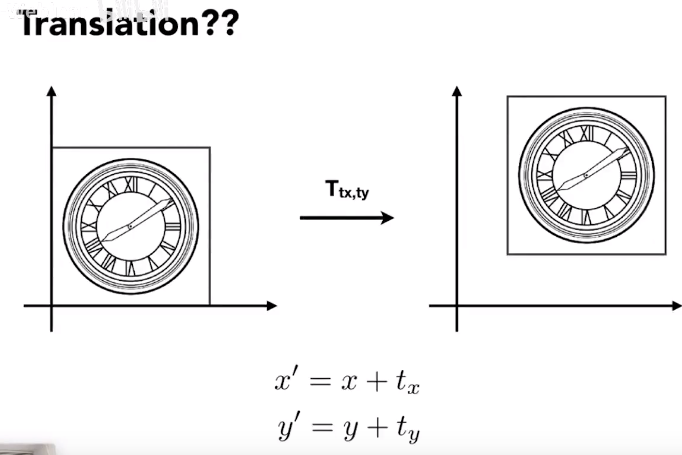
平移不是线性变换,我们不希望平移是一种特殊的变换
引入齐次坐标的cost是什么?

增加维度w 引入齐次坐标
向量具有平移不变性 What if you translate a vector?

《计算机图形学(OpenGL版)》的作者F.S. Hill Jr.曾说过一句话:
齐次坐标表示是计算机图形学的重要手段之一,它既能够用来明确区分向量和点,同时也更易用于进行仿射(线性)几何变换
于是我们知道,其重要性,主要有二,其一是区分向量和点,其二是易于进行仿射变化(Affine Transformation)

point+point = 齐次坐标系下 两点的中点
仿射变换
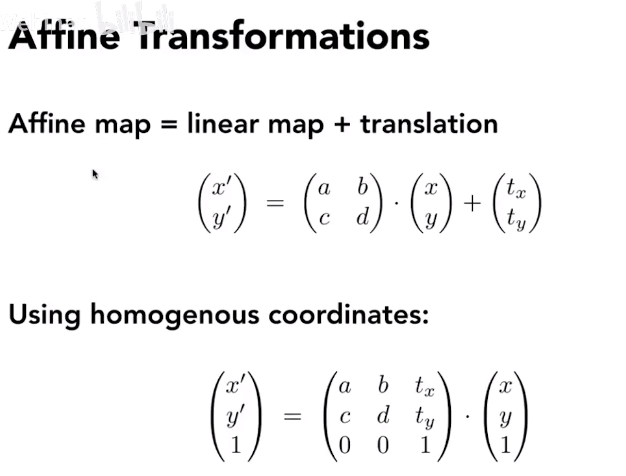
2D Transformation
S(Sx,Sy) R(α) T(tx,ty)

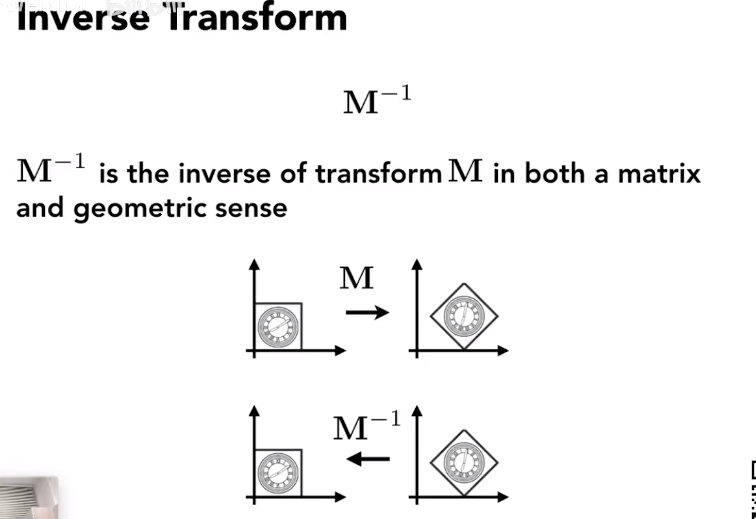
逆变换
组合变换
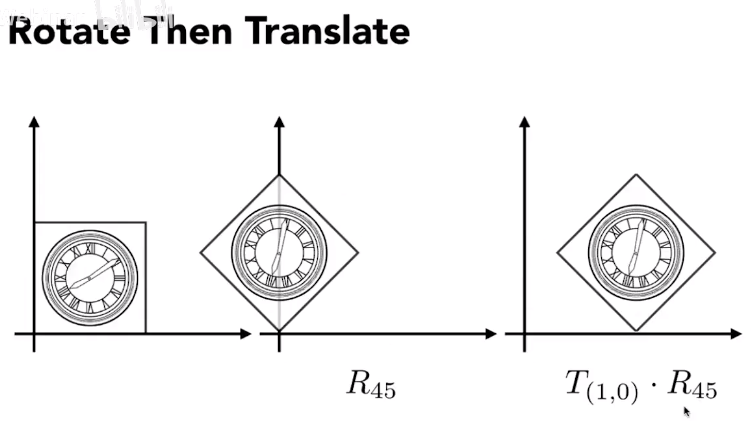
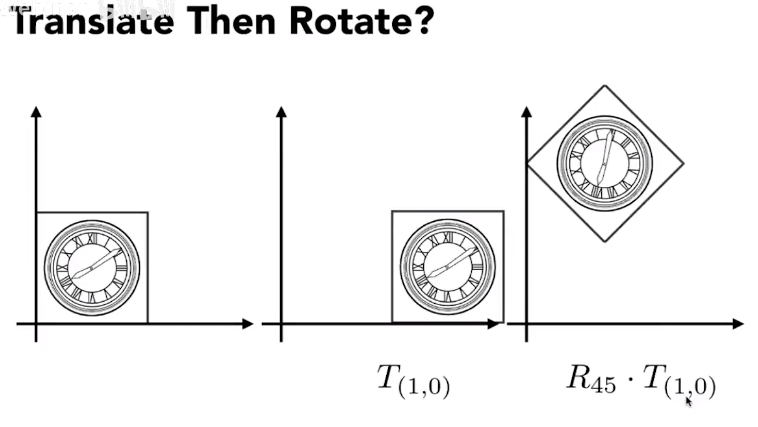
矩阵顺序:
$$
\begin{equation}
T_{(1,0)} \cdot R_{45} \cdot 矩阵
\end{equation}
$$
如果不以原点进行旋转呢?
对矩阵进行分解
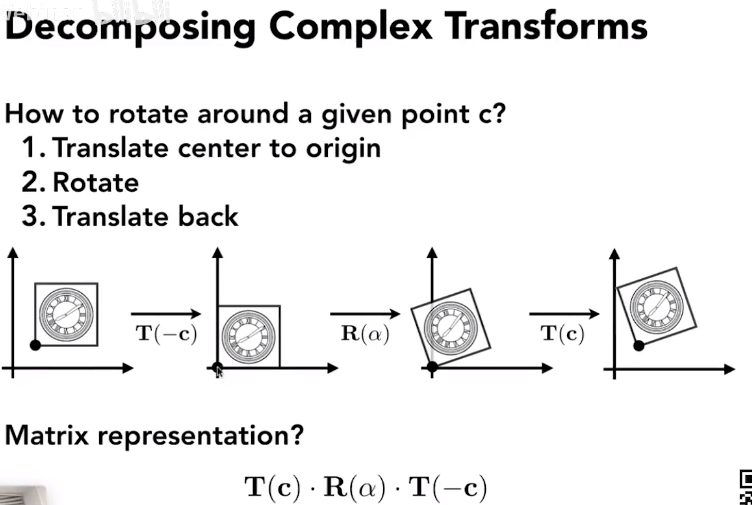
$$
\begin{equation}
\mathbf{T}(\mathbf{c}) \cdot \mathbf{R}(\alpha) \cdot \mathbf{T}(-\mathbf{c})
\end{equation}
$$
3维变换

先线性变换->后平移 平移对形状影响不大 可以放在最后 也可以写在矩阵最后一列进行组合


Transformation Cont
旋转矩阵的逆等于其转置 正交矩阵
scale translation
rotarion matrix
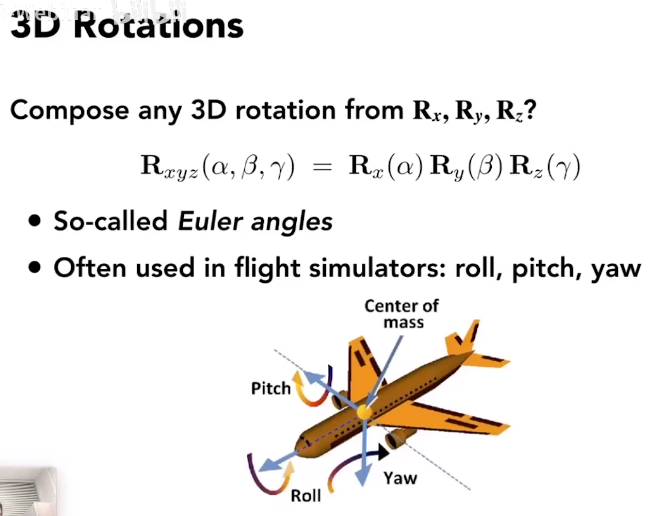
任意方向的旋转 欧拉角
绕任意轴旋转 formula

$$
\begin{equation}
\mathbf{R}(\mathbf{n}, \alpha)=\cos (\alpha) \mathbf{I}+(1-\cos (\alpha)) \mathbf{n} \mathbf{n}^{T}+\sin (\alpha) \underbrace{\left(\begin{array}{ccc}
0 & -n_{z} & n_{y} \
n_{z} & 0 & -n_{x} \
-n_{y} & n_{x} & 0
\end{array}\right)}_{\mathbf{N}}
\end{equation}
$$
视图变换
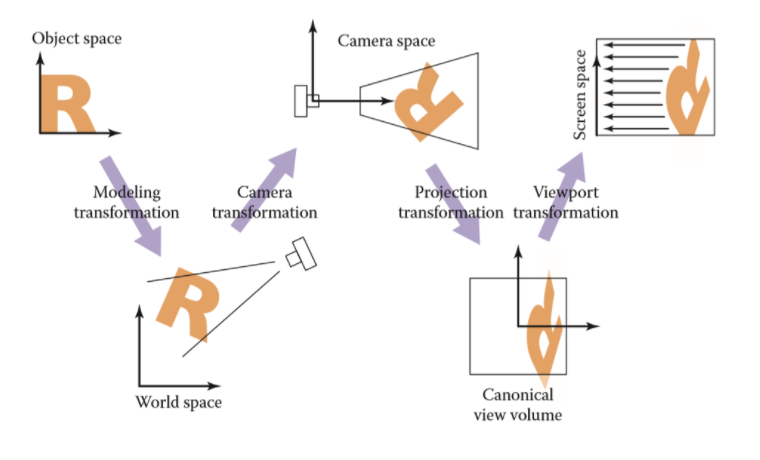
modeling tranformation 模型变换
将虚拟世界中或者更具体点,游戏场景中的物体调整至他们应该在的位置
View Camera tran. 相机变换
MVP 三变换 得到物体与摄像机的相对位置
摄像机变换的目的是得到所有可视物体与摄像机的相对位置,把物体和摄像机一起做移动,如果能够把摄像机的坐标轴(假设为u,v,w 分别对应原世界空间中的x,y,z)移动到标准的x,y,z轴,那么此时物体的坐标自然是相对坐标。
因此核心问题就变成了如何表示或者说如何将camera的坐标系与原世界坐标系重合
定义3个东西
- 相机或眼睛位置 (eye postion) e
- 观察方向 (gaze postion) g
- 视点正上方向 (view-up vector ) t
相机的三个属性

其中u,v,w分别对应标准坐标系下的x,y,z,示意图如下:

不直接拿 t 当做基底向量是因为摄像机的头可能是歪着看的
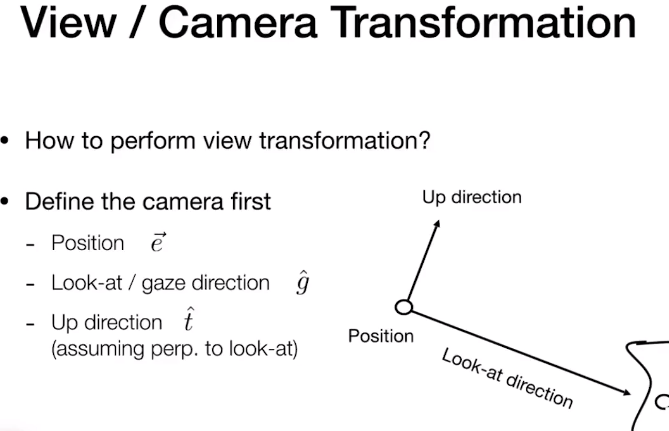
约定相机永远看向-Z方向,约定标准位置

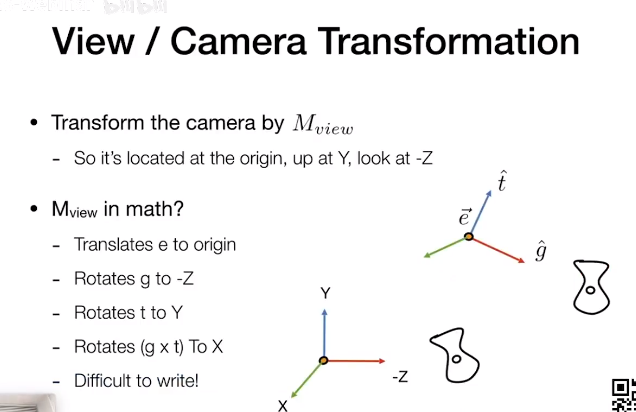
把相机的uvw移到xyz标准坐标去,朝向为-z轴
平移矩阵 平移相机位置到原点上去 和旋转矩阵

原始的旋转 从相机到世界原点的矩阵不好的到,反过来求其逆,把坐标原点旋转到相机,求逆就是其转置,因为旋转矩阵是
正交矩阵,就如同在blender里按下0到相机的视角。
Projection tran. 投影变换
正交投影Orthographic projection 和透视投影 Perspective projectivre
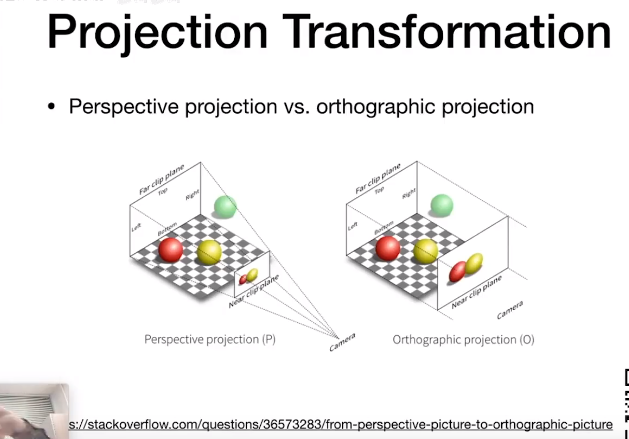
锥与正方体的区别,坐标标准化,正交投影直接把z坐标给扔掉就是正交投影的视图
正交投影
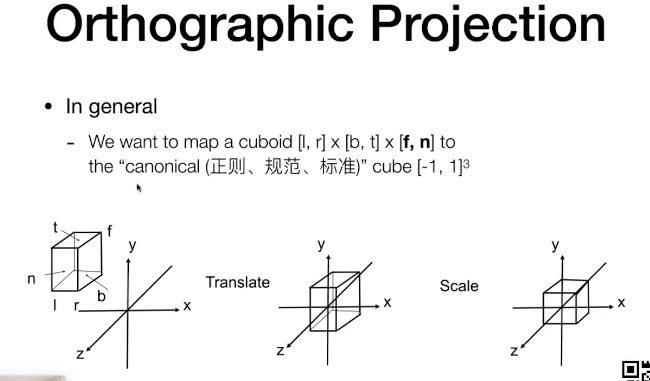
[left.right] [button,top] []
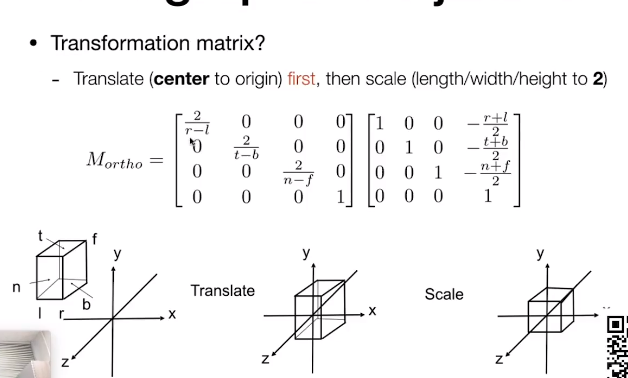
矩阵平移缩放标准化
透视投影

齐次坐标的缩放不变性

远平面到近平面的矩阵变换,从侧视图想起

一句逻辑推出x和y的解答 z的部分设为未知

推理出来矩阵的第1,2,4行只剩第3行的值

z用n代替 矩阵第三行乘原点得到n^2,但是A,B可能等于0,只有这一个条件还不行

使用原平面的中心点得到第二个约束条件

解的透视投影矩阵

作业0:
1.添加->正方体
2.面->交集(切割)
3.网格->分离->按松散块