GAMES101-Lecture02 Review of Linear Algebra笔记

旋转的例子

图形学中向量的默认形式是列向量

叉乘公式

$$
\vec{a} \times \vec{b}=\left(\begin{array}{l}
y_{a} z_{b}-y_{b} z_{a} \\
z_{a} x_{b}-x_{a} z_{b} \\
x_{a} y_{b}-y_{a} x_{b}
\end{array}\right)
$$

$$
\vec{a} \times \vec{b}=A^{*} b=\left(\begin{array}{ccc}
0 & -z_{a} & y_{a} \\
z_{a} & 0 & -x_{a} \\
-y_{a} & x_{a} & 0
\end{array}\right)\left(\begin{array}{l}
x_{b} \\
y_{b} \\
z_{b}
\end{array}\right)
$$

$$
\begin{array}{l}
\vec{x} \times \vec{y}=+\vec{z} \\
\vec{y} \times \vec{x}=-\vec{z} \\
\vec{y} \times \vec{z}=+\vec{x} \\
\vec{z} \times \vec{y}=-\vec{x} \quad \vec{a} \times(\vec{b}+\vec{c})=\vec{a} \times \vec{b}+\vec{a} \times \vec{c} \\
\vec{z} \times \vec{x}=+\vec{y} & \vec{a} \times(k \vec{b})=k(\vec{a} \times \vec{b}) \\
\vec{x} \times \vec{z}=-\vec{y}
\end{array}
$$
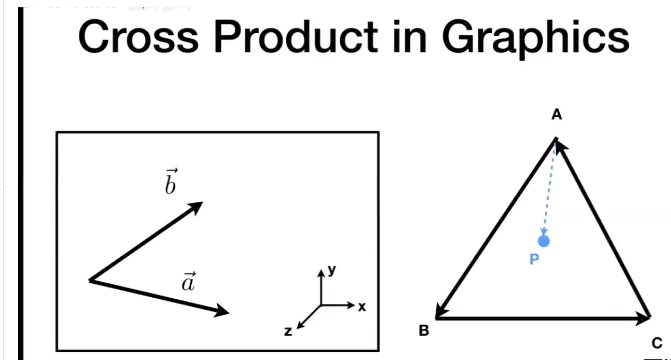
叉乘可以定义左右和形状的内外两侧信息，起到定向的作用

$$
\begin{array}{l}
\vec{a} \times \vec{b}=+\vec{z} \quad \quad a在b的左侧 \\
\vec{b} \times \vec{a}=-\vec{z} \quad \quad a在b的右侧\\
\vec{AB} \times \vec{AP}=+ \\
\vec{BC} \times \vec{BP}=+ \\
\vec{CA} \times \vec{CP}=+ \quad \quad 如P点在AC右侧,则\vec{CA} \times \vec{CP} 为负值 \\
如三角行逆时针,只要所有的叉乘值都为正值或都为负值就可判断在三角形内部，从而忽略给定的三角形的顺序 \\
在边上的情况被称为 corner case 这时候开发者自己说了算\
\\
\end{array}
$$

虚拟机安装问题

Not in a hypervisor partition (HVP=0) (VERR_NEM_NOT_AVAILABLE).

AMD-V is disabled in the BIOS (or by the host OS) (VERR_SVM_DISABLED).

解决方法

1.Windows设置 - 更新和安全 - 回复 - 立即重新启动

2.Troubleshoot -> Advanced option – > UEFI Firmware Settings -> Restart

3.在BIOS中找到Virtualization 选项，它常位于Advanced 或 System Configuration 选项卡下

4.设置Virtualization 的状态为Enabled。

AMD和Intel的设置不一样

Eigen库的使用问题

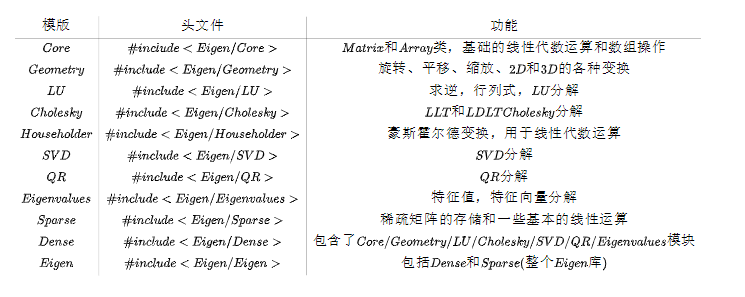
Eigen库的使用用例

#include<cmath>

#include<iostream>

#include "../../Eigen/Core"
#include "../../Eigen/Dense"

int main()
{
    // Basic Example of cpp
    std::cout << "Example of cpp \n";
    float a = 1.0, b = 2.0;
    std::cout << a << std::endl;
    std::cout << a / b << std::endl;
    std::cout << std::sqrt(b) << std::endl;
    std::cout << std::acos(-1) << std::endl;
    std::cout << std::sin(30.0 / 180.0 * acos(-1)) << std::endl;

    // Example of vector
    std::cout << "Example of vector \n";
    // 向量定义
    Eigen::Vector3f v(1.0f, 2.0f, 3.0f);
    Eigen::Vector3f w(1.0f, 0.0f, 0.0f);
    // 向量输出
    std::cout << "Example of output \n";
    std::cout << v << std::endl;
    // 加法
    std::cout << "Example of add \n";
    std::cout << v + w << std::endl;
    // 点成
    std::cout << "Example of scalar multiply \n";
    std::cout << v * 3.0f << std::endl;
    std::cout << 2.0f * v << std::endl;

    // Example of matrix
    std::cout << "Example of matrix \n";
    // 矩阵定义
    Eigen::Matrix3f i, j;
    i << 1.0, 2.0, 3.0, 4.0, 5.0, 6.0, 7.0, 8.0, 9.0;
    j << 2.0, 3.0, 1.0, 4.0, 6.0, 5.0, 9.0, 7.0, 8.0;

    // 矩阵输出
    std::cout << "Example of output \n";
    std::cout << i  << std::endl;
    std::cout << j << std::endl;
	//矩阵加法
    std::cout << " matrix add matrix i + matrix j" << std::endl;
    std::cout << i+j << std::endl ;
    //矩阵点乘
    std::cout << " matrix scalar multiply i * 2.0" << std::endl;
    std::cout << i*2.0 << std::endl;

    //矩阵乘法
    std::cout << "matrix multiply i * j" << std::endl;
    std::cout << i * j << std::endl;

    std::cout << "matrix multiply vector i * v" << std::endl;
    std::cout << i * v << std::endl;
    std::cout << v.transpose()*i << std::endl;//reslut is different 
    //14
    //32
    //50

    //Transpose result is 30 36 42


    return 0;
}