1.同构


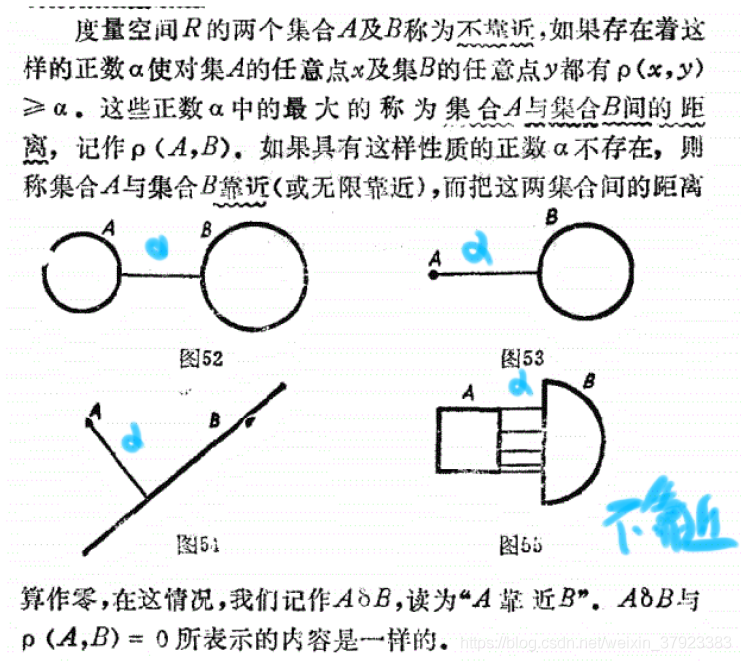
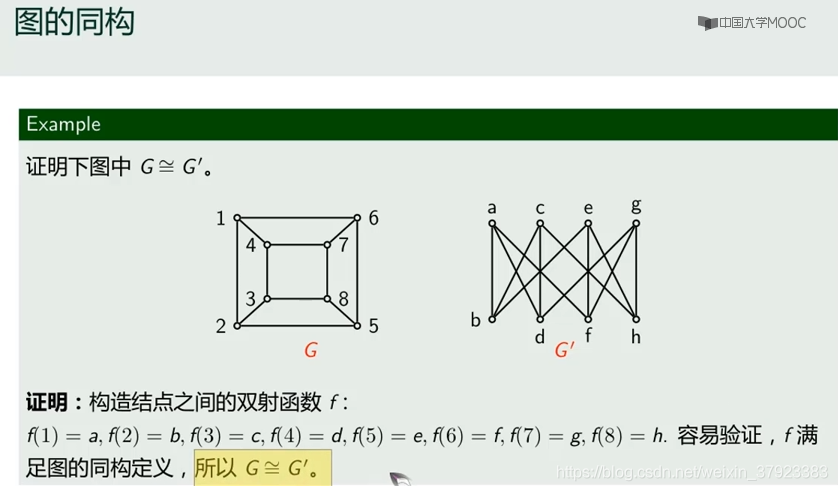
1.1图的同构

2.距离的概念
度量:度量就是距离,但是空间本来没有距离。比如我构造一个空间A-(题主,答主,回复者,知乎管理员},这个空间一开始就没有距离的概念。同样的,我们生活的3维空间一开始也没有距离的概念,每个点都可以看做孤立的点,整个空间可以看做这些点的集合。
那距离是什么呢?距离是人类加在空间上的一种关系:任意两个点映射到一个实数。任何满足条件的这种映射都可以叫距离(正定性,对称性,三角不等式)。比如对于刚才的空间A,我定义一个距离:同一个人距离等于0,不同人的距离等于1。这就构成了一个有距离的空间(度量空间),A空间中,以题主为球心,半径为1的球面就是(答主,回复者,知乎管理员)
那么, n维欧氏空间中两点的距离是什么呢?和3维的情形一样:坐标相减,平方和,开根号。反过来, n=3时的球面就和我们通常见到的球面一样。
距离是用于表示两个物体间的远近,是存在于两个物体之间的一种关系,我们就可以对集合中的每一对元素指定一个数字,这个数字就代表两个物体之间的距离。
需要注意的是,在现实生活中,距离都是有米、厘米之类的单位,而度量空间中则不存在这些单位,所有的距离都是实数。
3.度量空间

3.1 度量空间两点之间的距离

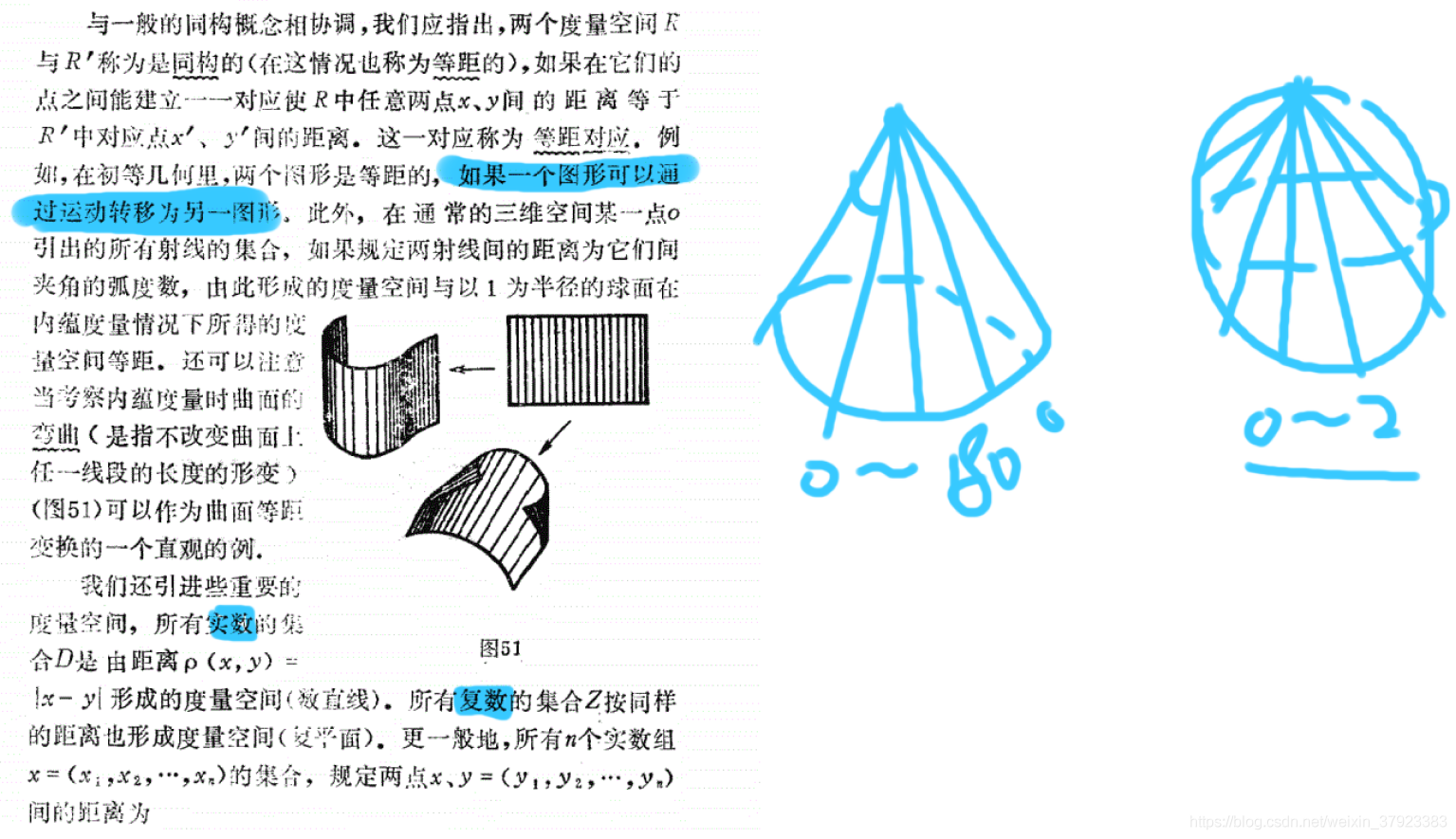
3.2 度量空间等距(同构)

3.3 集合间的距离
3.4 集合间的靠近与不靠近