1.射影平面定义

2.摄像机与地面上的三角形
图1。摄像机为投影中心,在地面上拍摄三角形ABC。这个地面是一个完美的平面。淡绿色的区域是从相机上看到的。从相机发出的黑色光线表示取景器的立体区域(金字塔)。在黑色光线上安装的方形板是为了显示我们可以通过相机看到的东西。让我们把这个正方形的板子叫做屏幕。三角形ABC在地面上的照片被拍成屏幕上的三角形A’ b ’ c`。白光是三角形顶点的投影线。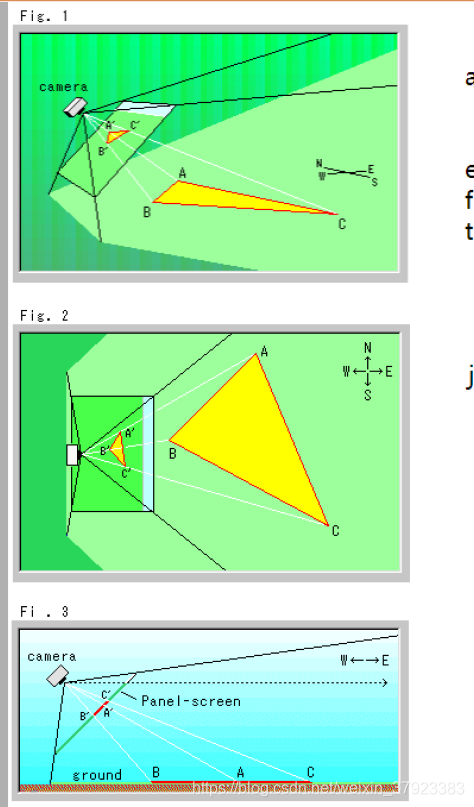
依旧,图2是俯视图的情况,而图3是侧视图。
图4是拍摄视角的试视图,而根据图可以看出经过射影变换之后的直线是不变的。虽然经过射影变换之后三角形的形状和大小会变化,但是直线依旧是直线。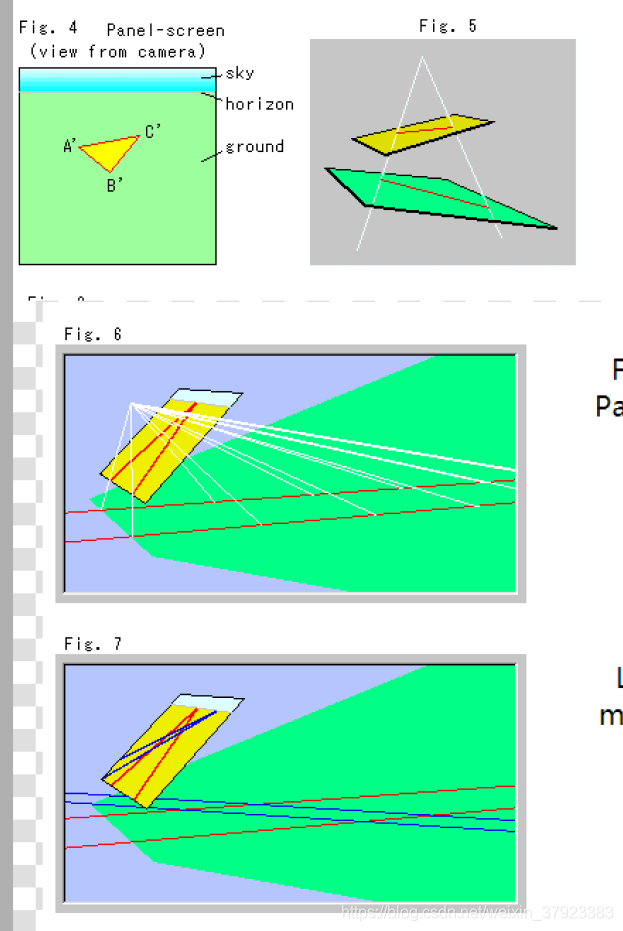
图6是平行线的投影。面板屏幕上的平行线看起来有端点,并在地平线上相遇。
图7画了两对平行线,将它们投射到面板屏幕上。同时,蓝色平行直线也在水平线上相交。
3.摄影机视角的平行线
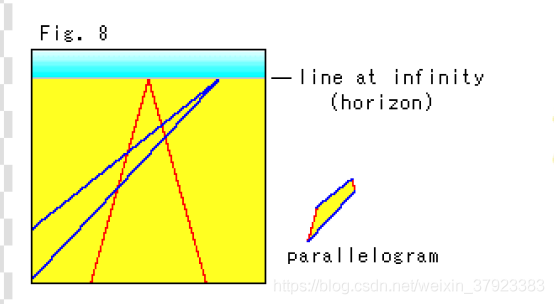
图8显示了面板屏幕上的两对平行线。右下角是它们构成的平行四边形。数学家把平板屏幕上的视界称为无穷远处的一条线。然而,没有这样的物理线存在。这个名字很不合适。它混淆了初学者。它不是一条无限远的直线。我们只能在面板屏幕上捕捉到它作为地面和天空的边界。换句话说,无穷远处的线是人造的,那条线其实在现实中并不存在。
4.180°摄影机
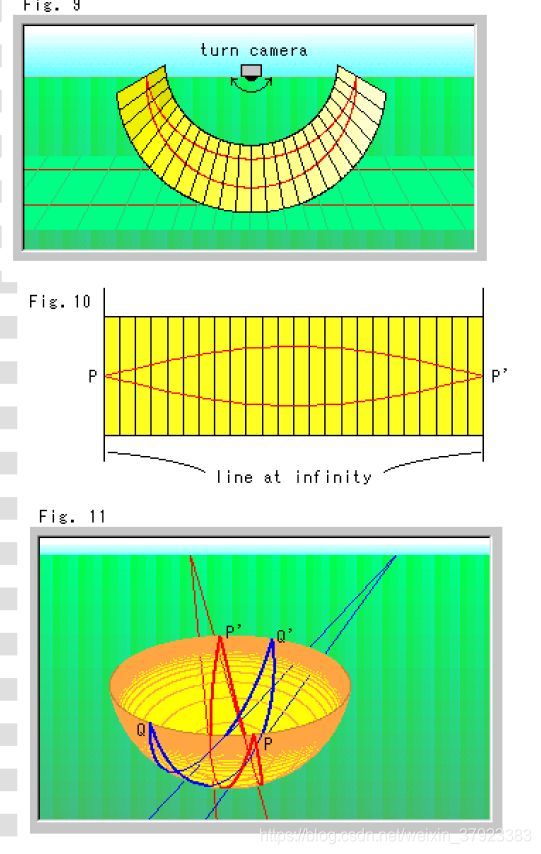
图9显示了180°相机与矩形平面的拍摄。平面形成半圆柱体。帮助我们得到整个平行线范围的全图。地面上的平行线看起来像铁路,但在屏幕上则不然。
图10显示了图9的展开面板屏幕。点P和P’在无穷远处(视界)线上。面板屏幕是全景的,很好的看到一对平行线。但对于平行线间距大的情况就不方便了。它不能覆盖不同方向的直线。
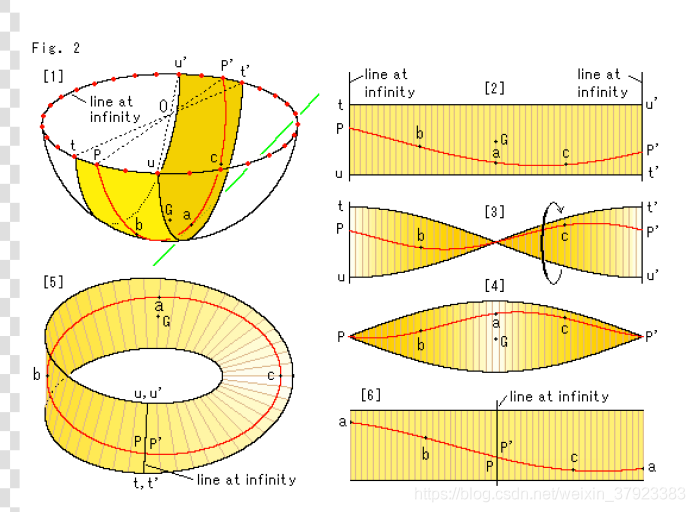
图11显示了球面上的两对平行线。它们从地面投射到一个半球。半球的中心是投影中心。半球的边缘(赤道的周长)现在是一条无限远的线。
吐槽:有一说一,射影平面确实是由摄影来的(
5.莫比乌斯环( Mobius Strip)
球面直径两端相对的两点称为对跖点。在一个半球的边缘有无数对映点。所有由地面中心投影形成的半球边缘对映点都必须被识别出来。也就是说,无限展开的地面有一些类似于对映点的东西。这个平面就是射影平面。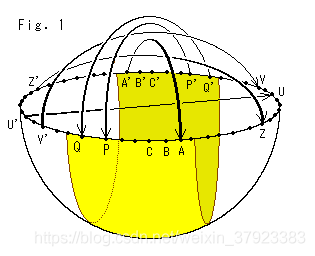
其经过变化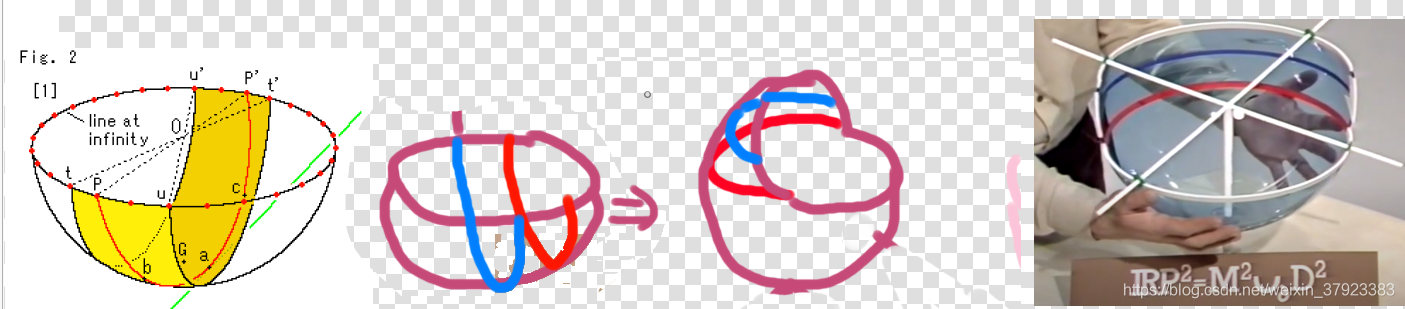
经过简化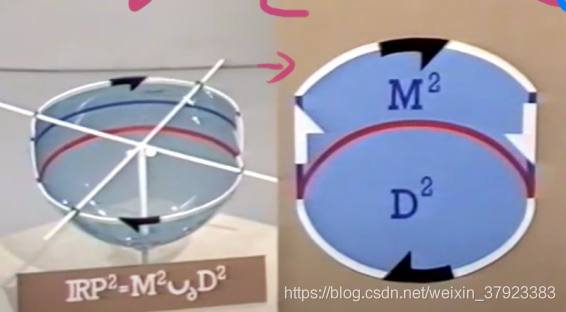

6.不可定向曲面包含莫比乌斯环

7.投影平面上的线与莫比乌斯环的比较
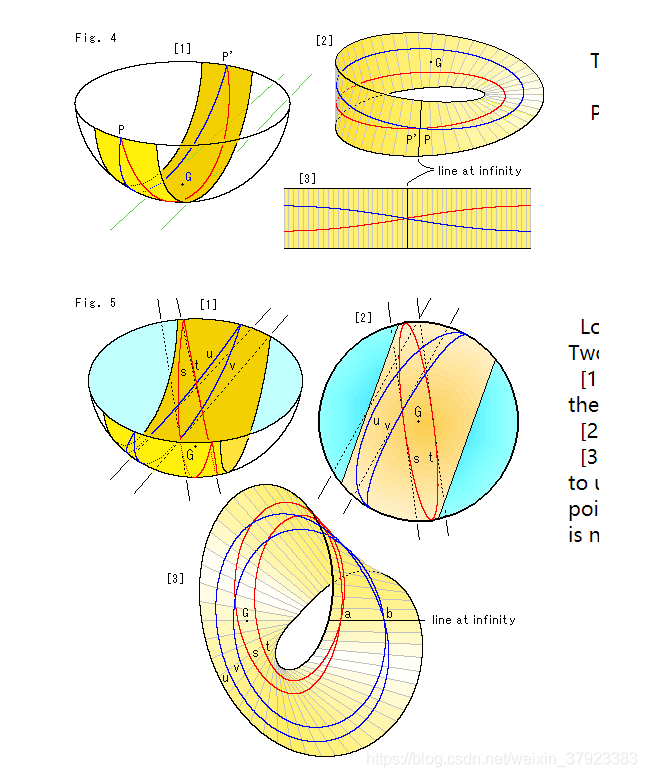
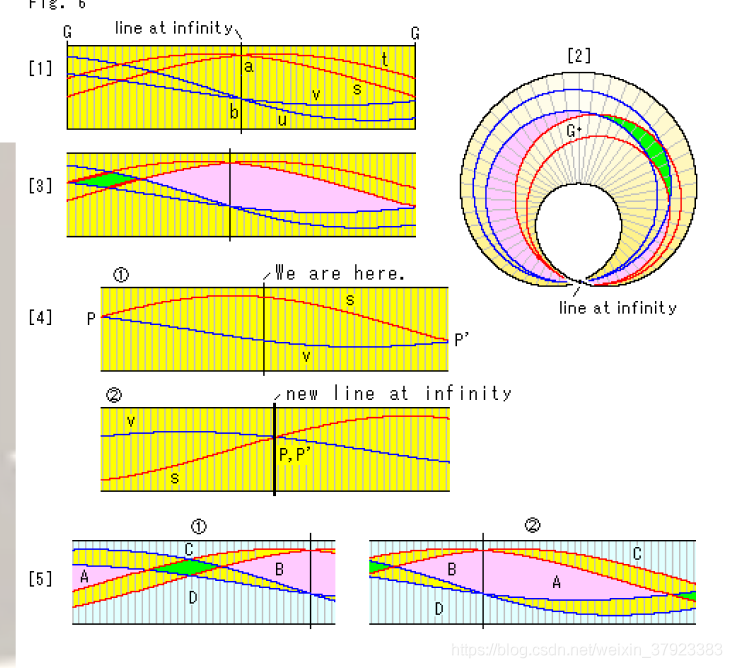
参考:
Projective Geometry (1)
M335 TV3 The Projective Plane RP2 (with Colin Rourke) (Geometric Topology)