基础拓扑学笔记(3)--连续映像

1.问题:什么叫连续？什么叫连续映射，研究拓扑为什么需要连续映射？

每门学科都建立在一些基础概念上，而拓扑学中贯穿着一个概念，就是连续性的概念。

要说明连续的概念，要从函数连续的概念类比。

2.函数=一个量依赖于另一个量

3.量的取值要有意义

这些有意义的所有值的集合起了个名字叫做定义域

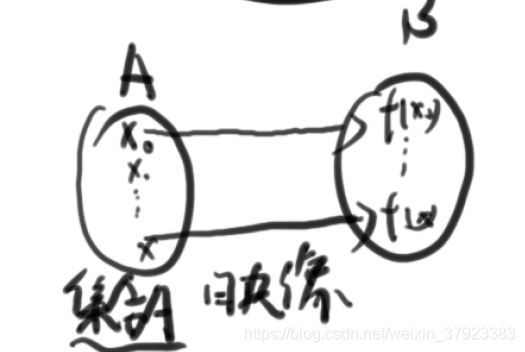
4.集合并非只有实数组成

5.f(x)在x0处连续

连续的定义表达需要用到极限，极限需要用到距离的概念，也就是说只有先定义了距离，才能有极限，才能定义连续，连续可以用极限来表示，也可以用文本的概念来表述。

极限定义的连续如下:

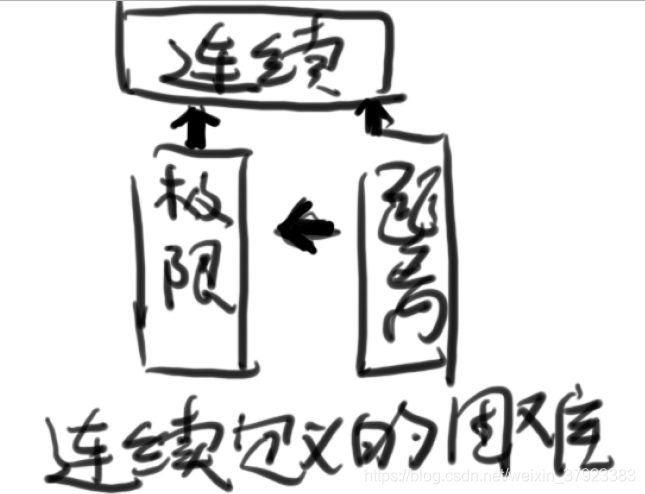
6.由距离引出邻域的概念

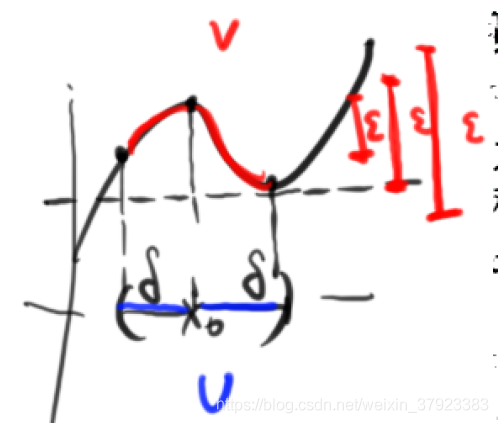
7.邻域引出连续映射的概念

将邻域从实数域扩展出来，邻域概念是连续映射概念的基础，就如同只有定义了距离才能定义连续函数一样。

对比之前函数连续的定义，将函数域中的距离概念用邻域来替代，范围更加广阔，距离是邻域概念在实数域的一个小名，对于实数域来说，邻域就是距离概念，距离就是邻域，而现在要扩展到更广阔的空间，而这个空间没有距离的概念。

8.不是函数但是是映射

函数是一一对应的，但是映射并不一定。
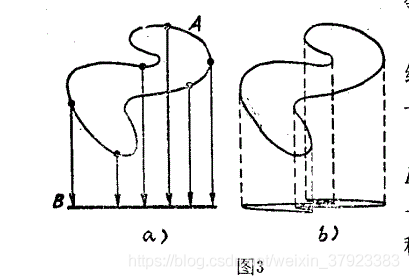
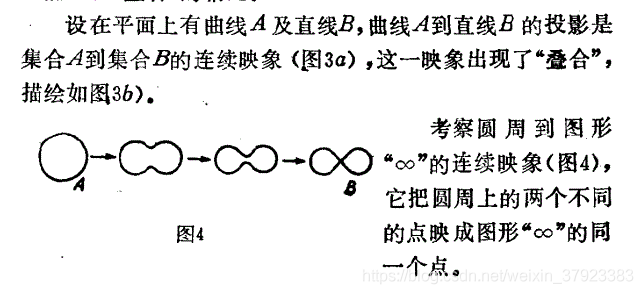
下面是连续映像出现叠合的情况。