基本拓扑学=1/3点集拓扑+2/3 代数拓扑
微分几何 微分流形
1.顶点数-棱数+面数 = 2

V=Vertex 顶点数 E= Edge 边数 F=Face 面数
2.凹多面体与凸多面体
多面体:若干个多边形沿着边粘出来的曲面所围成的立体、
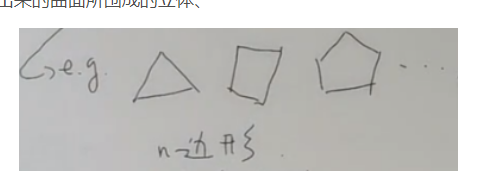
凸多面体的任何截面都是凸多边形,与凹多面体相反。
把凸多面体的任何一个面伸展成平面,它的所有其他各面都在这个平面的同侧。

3.欧拉定理的弱化版本(凸多面体)
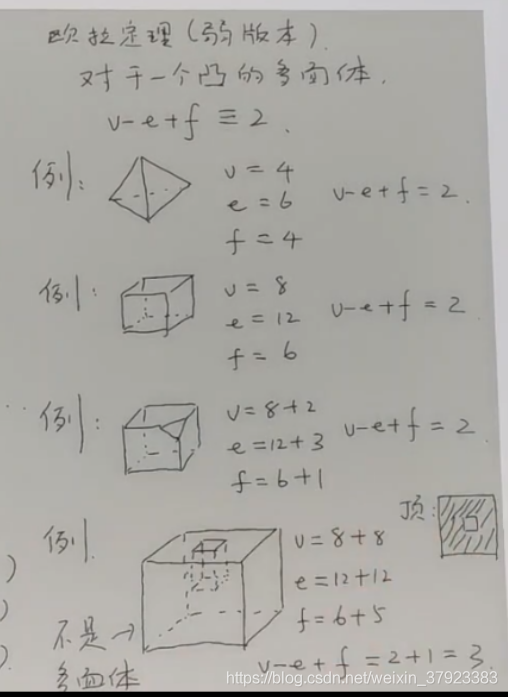
最后一个计算没有意义因为顶面的形状不算是多边形,也就说其形状并非多面体。为满足多面体的定义当然不满足欧拉定理
但是如果加几条边的话,使得围成的图形都是多边形在进行计算则满足欧拉定理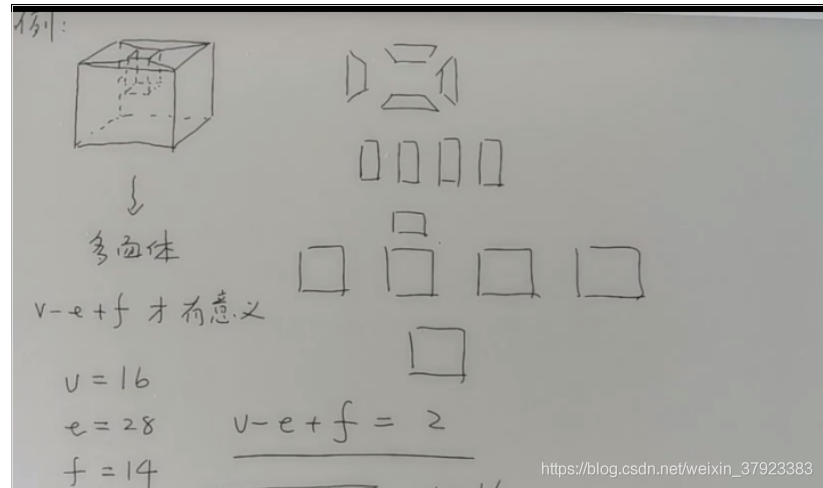
4.挖穿的洞
如果把上面的正方体所凿出的洞挖透会如何?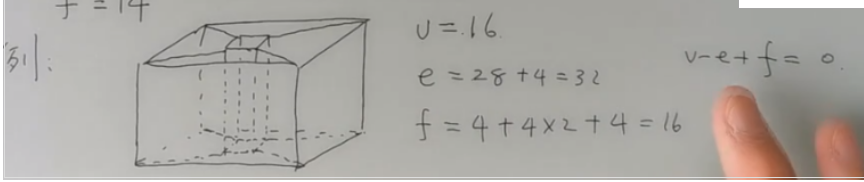
结果会变成V-e+f=0
5.问题
例1-4 为何v-e+f相同?
例5为何v-e+f与1-4不同,其本质区别是什么?
答案: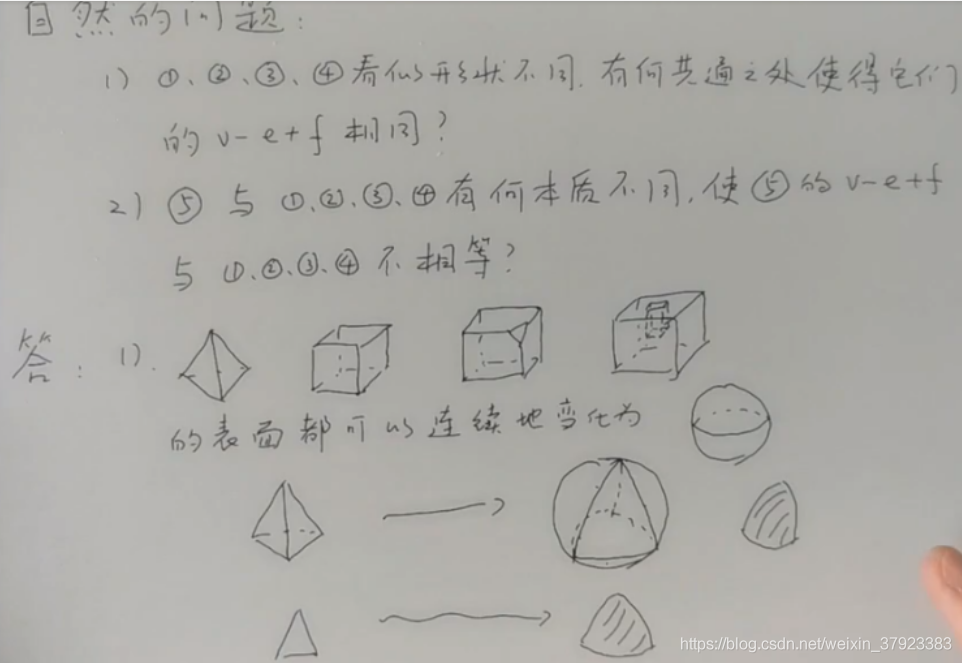
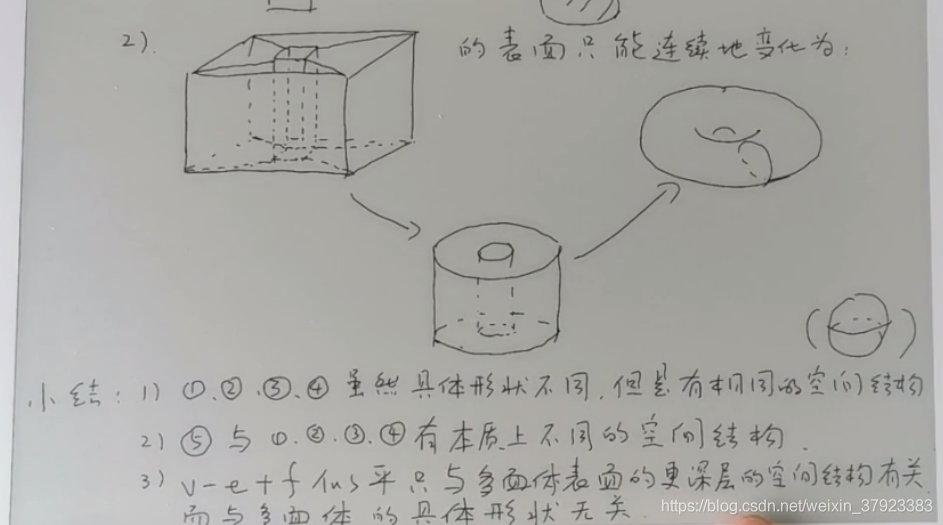
例1-4可连续变化为球面
例5可变化为轮胎面
也就是说欧拉定理与具体的几何形状无关,而更深层的几何结构有关
6.推广为更一般的定理(n个洞)



7.另一个特性 闭形式与恰当形式
光滑函数(smooth function):在其定义域内无穷阶数连续可导的函数。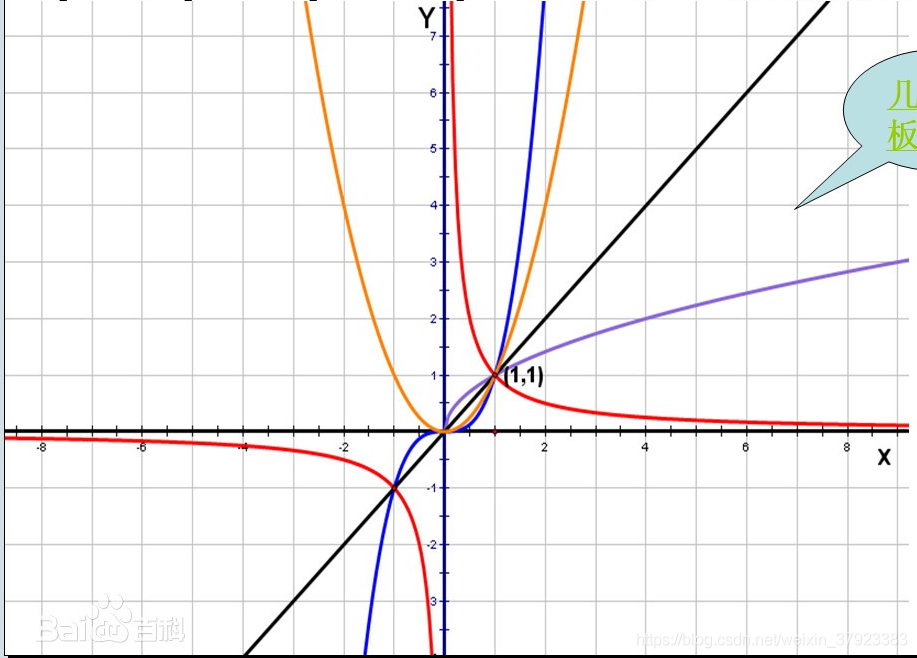
例如,指数函数显然是光滑的,因为指数函数的导数是指数函数本身。
因为没学过这个闭形式是否为恰当形式 ,有点听不懂,之后补上笔记。
参考:
基础拓扑学(a first course in topology)