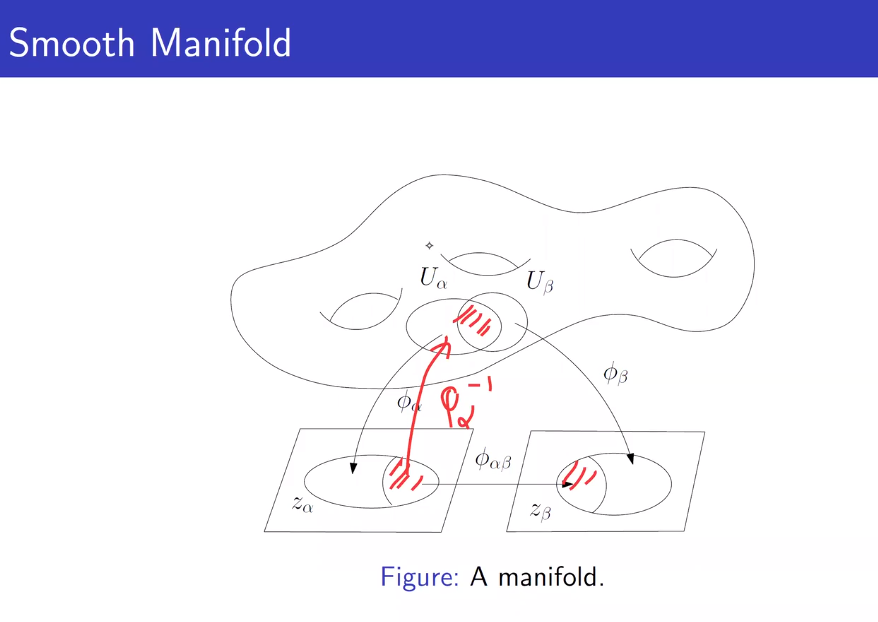
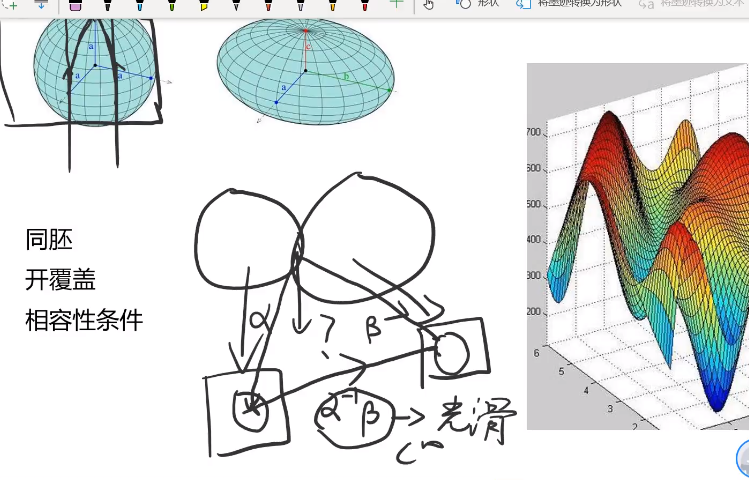
布劳威尔(Brouwer)不动点理论
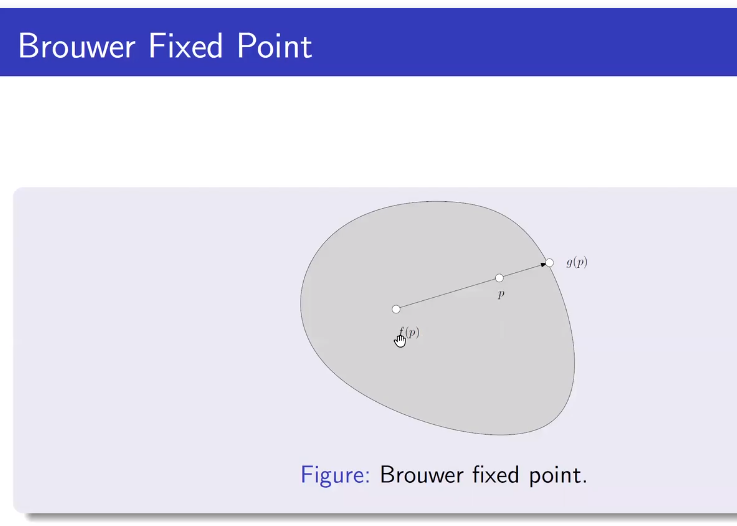
对于一个拓扑空间中满足一定条件的连续函数f,存在一个点x0,使得f(x0) = x0。
这个定理可以通过很实际的例子来理解。比如:取两张一样大小的白纸,在上面画好垂直的坐标系以及纵横的方格。将一张纸平铺在桌面,而另外一张随意揉成一个形状(但不能撕裂),放在第一张白纸之上,不超出第一张的边界。那么第二张纸上一定有一点正好就在第一张纸的对应点的正上方。一个更简单的说法是:将一张白纸平铺在桌面上,再将它揉成一团(不撕裂),放在原来白纸所在的地方,那么只要它不超出原来白纸平铺时的边界,那么白纸上一定有一点在水平方向上没有移动过。
这个断言的根据就是布劳威尔不动点定理在二维欧几里得空间(欧几里得平面)的情况,因为把纸揉皱是一个连续的变换过程。
另一个例子是大商场等地方可以看到的平面地图,上面标有“您在此处”的红点。如果标注足够精确,那么这个点就是把实际地形射到地图的连续函数的不动点。
地球绕着它的自转轴自转。自转轴在自转过程中是不变的,也就是自转运动的不动点
如果我们用一个密封的锅子煮水,那么总有一个水分子在煮开前的某一刻和煮开后的某一刻处于同样的位置。
(Lefschetz)莱夫谢茨不动点定理
布劳威尔不动点定理是莱夫谢茨不动点定理的特例。
莱夫谢茨不动点定理是布劳威尔不动点定理的推广。
设|K|为有限多面体,f:|K|→|K|为连续映射,若f的莱夫谢茨数L(f)≠0,则f有不动点。

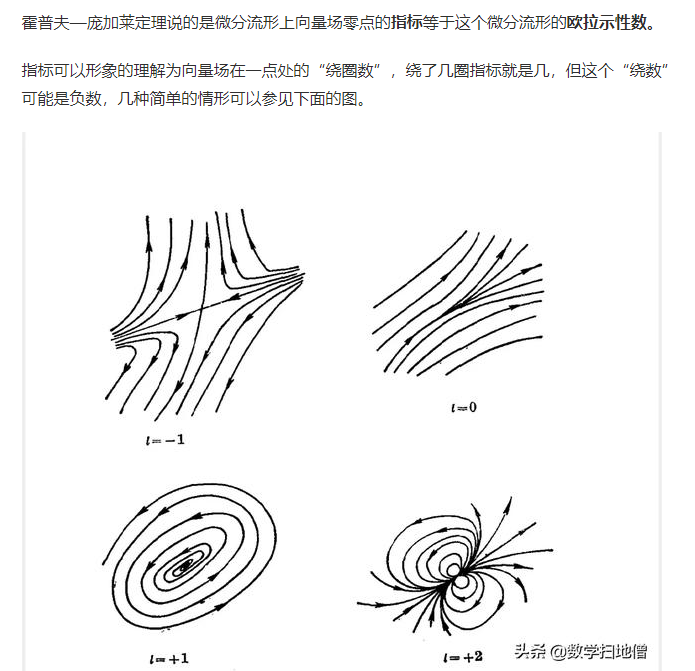
孤立零点

零点的指标

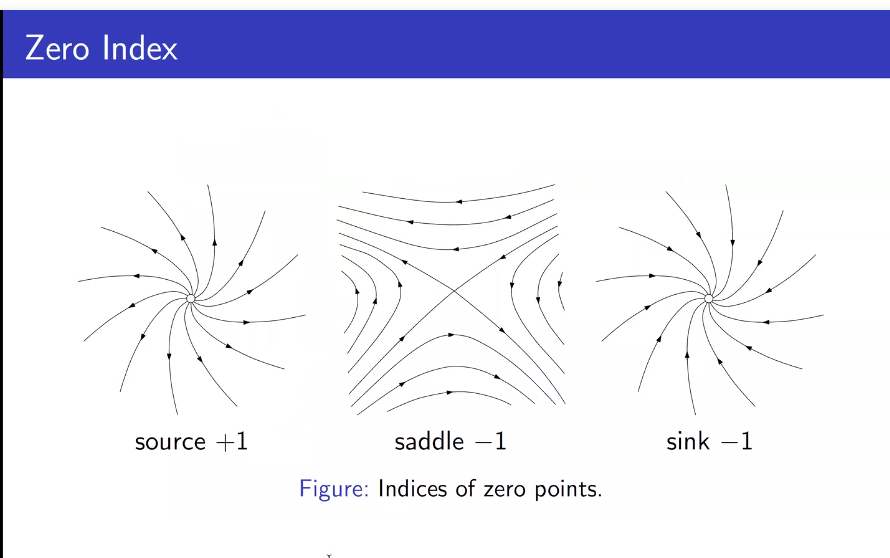
**庞加莱-霍普夫(Poincaré-Hopf)**定理
庞加莱-霍普夫(Poincaré-Hopf)定理(也称为庞加莱-霍普夫指标定理,庞加莱-霍普夫指标公式,或霍普夫指标定理)是微分拓扑的重要定理。


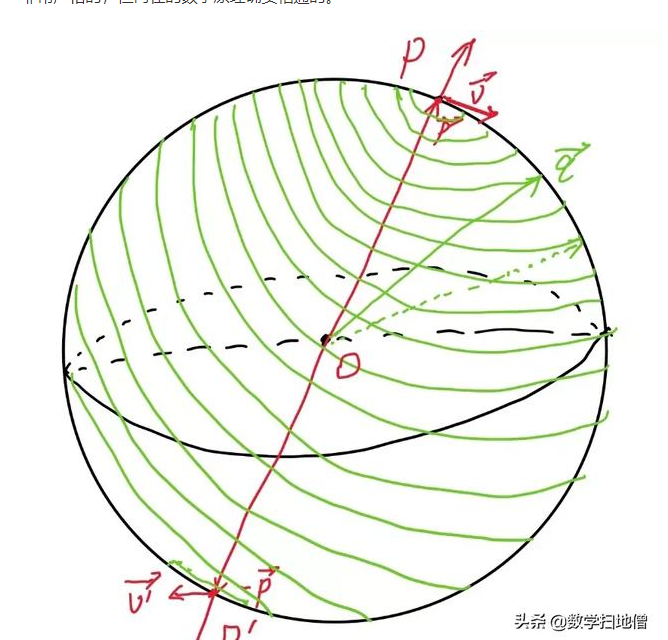
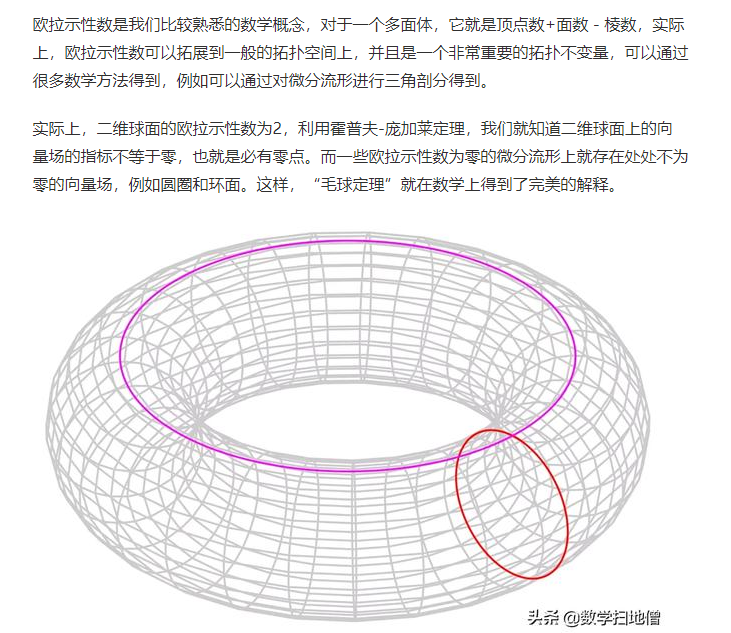
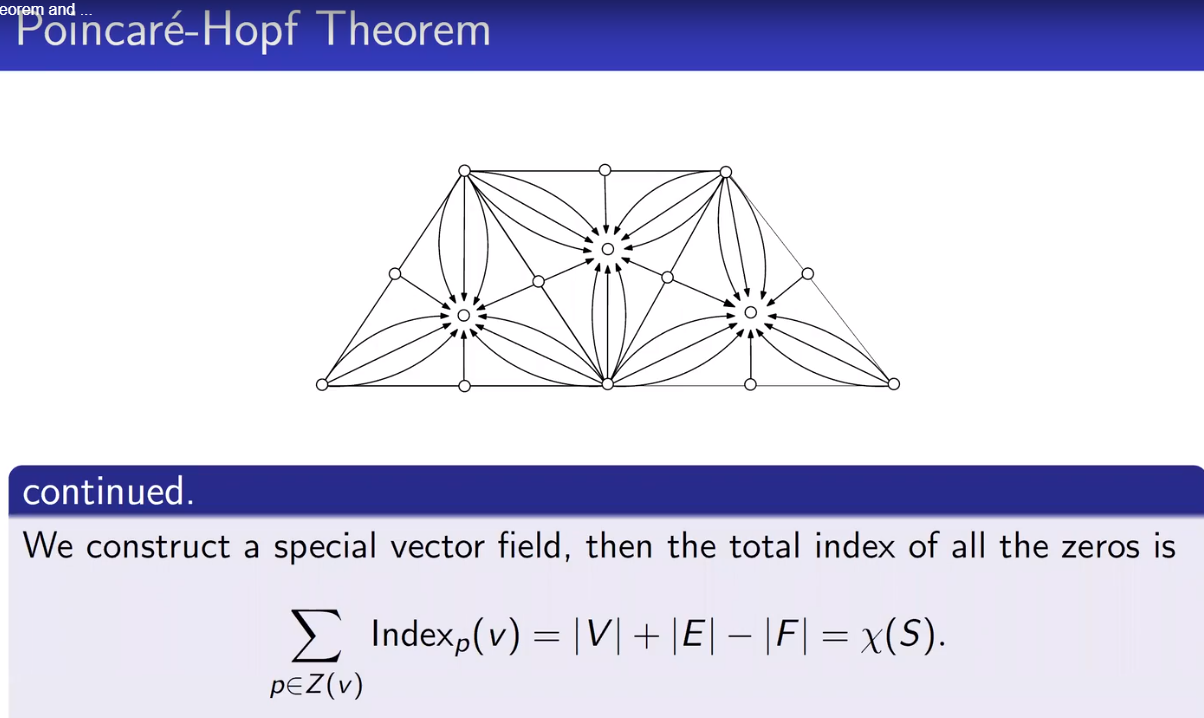
流形