Molers Blog

饱腹的鼹鼠

0%

共形几何第三节-同调群和上同调群Homology and Cohomology

发表于 更新于 分类于

闭合曲面的拓扑

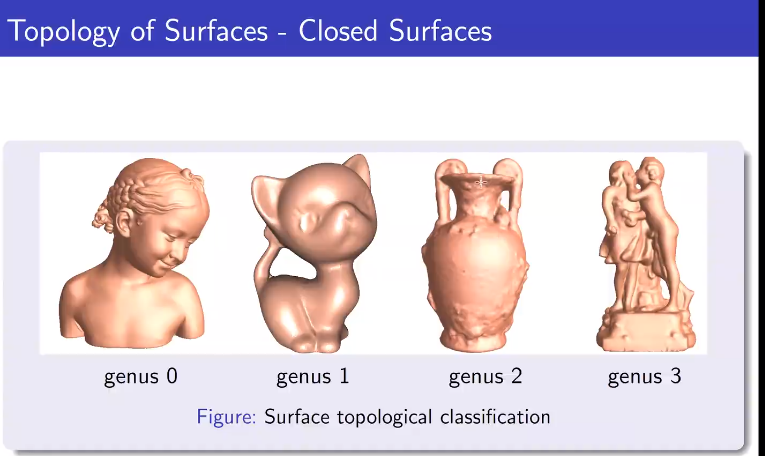
image-20200726113232194

带有边界的曲面的拓扑

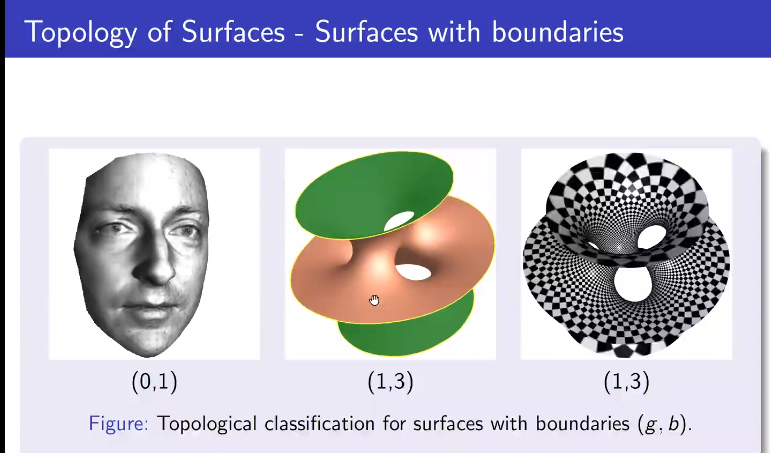
image-20200726113243216

g为洞的数目，b为边界的数目

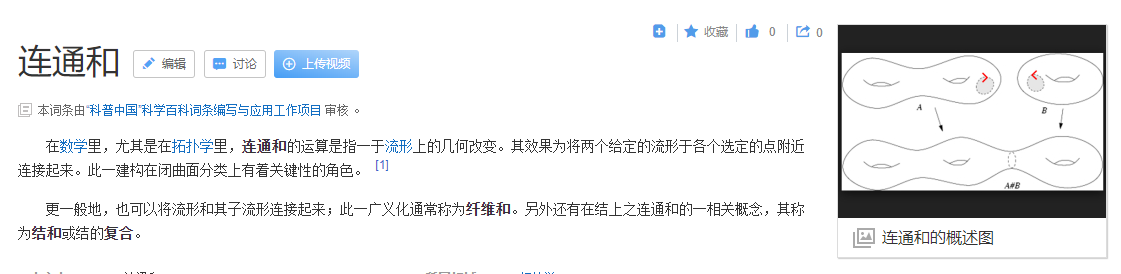
连通和

image-20200726114406417

image-20200726113912895

image-20200726113928708

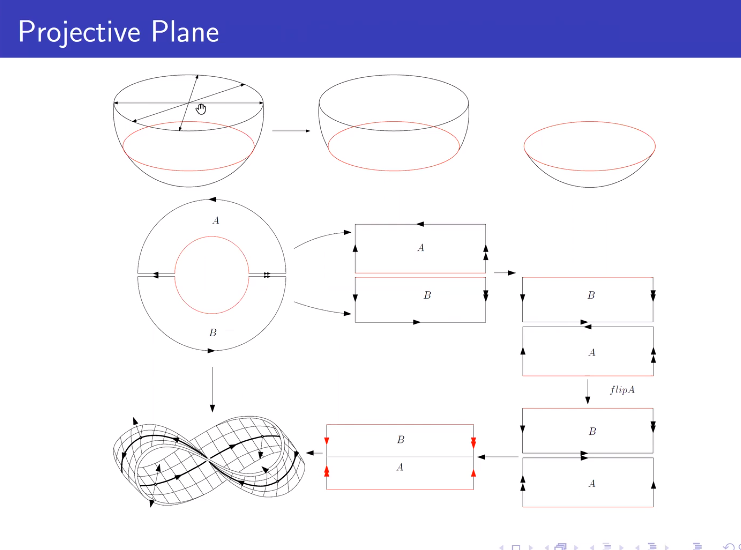
射影平面

image-20200726114220282

image-20200726114235740

image-20200726122603769

闭合曲面的连通和是可定向的曲面，而具有交叉的曲面的连通和是不可定向的

image-20200726212207039

一些基本连接面

image-20200726212717260

D Disk圆盘 S Sphere球体 T

可定向曲面和不可定向曲面连接和的代数表述

image-20200726213324643

image-20200726212852103

image-20200726213108274

image-20200726213152393

具有三个不同基本结构曲面的连接

image-20200726213216805

image-20200726212907797

image-20200726213041304

球体+环面 S#L

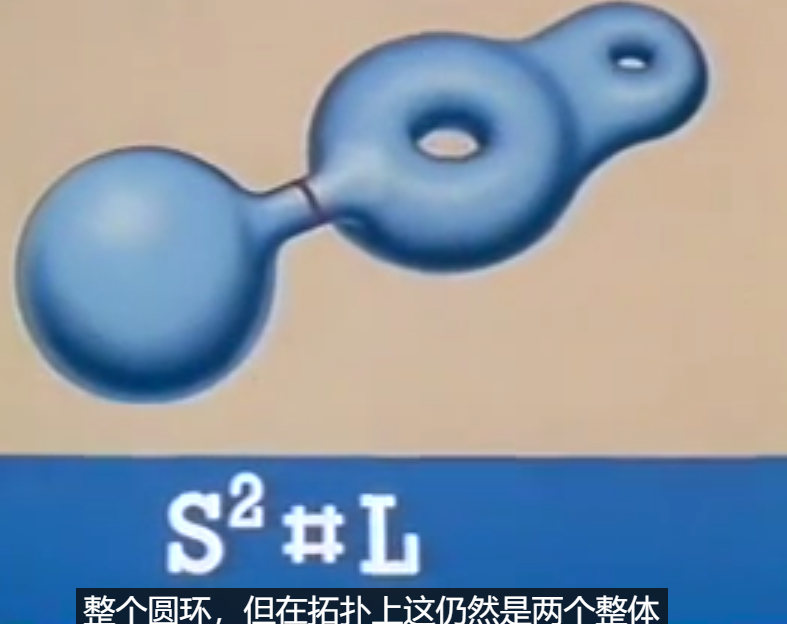
image-20200726213855932

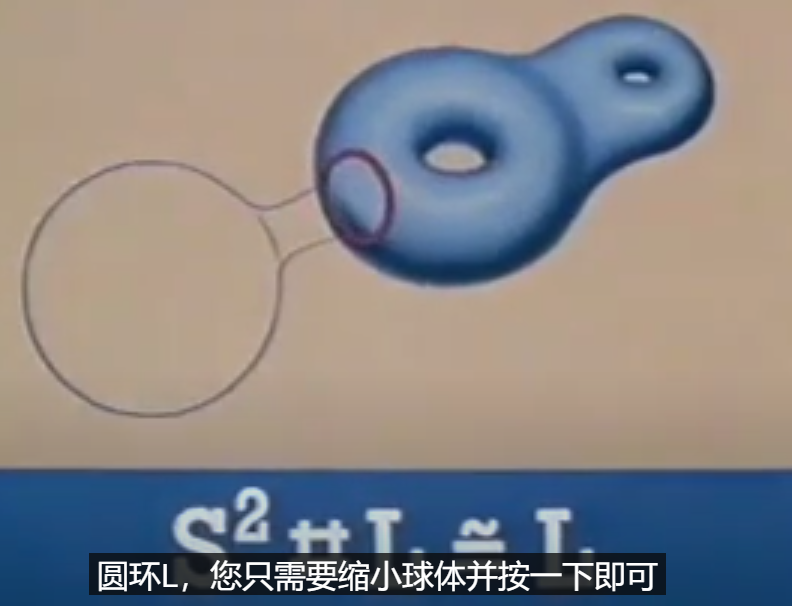
image-20200726213948575

其结果和环面同胚

实际上球体和任何曲面相连都是一样的

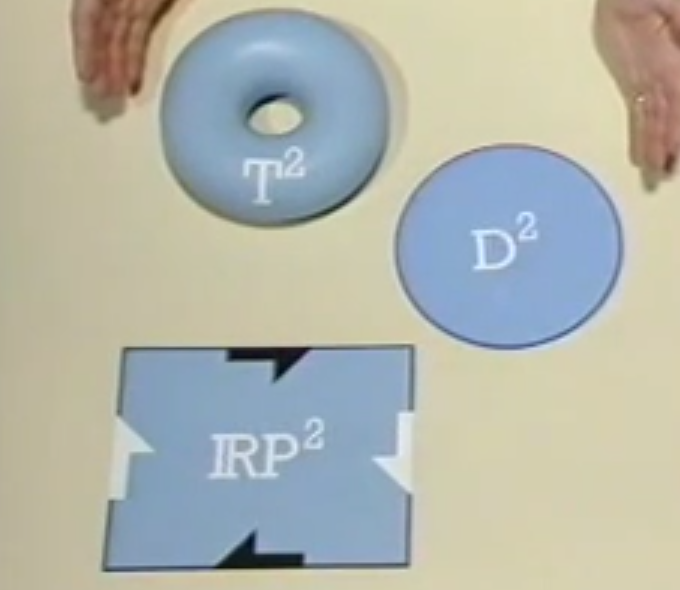
一个假设:球体以外的任何曲面都可以由T,D，IRP三种曲面组合而成

image-20200726214147520

圆环与莫比斯环 T\D # M\D

image-20200726214217713

image-20200726214323947

圆环的变形

image-20200726214347558

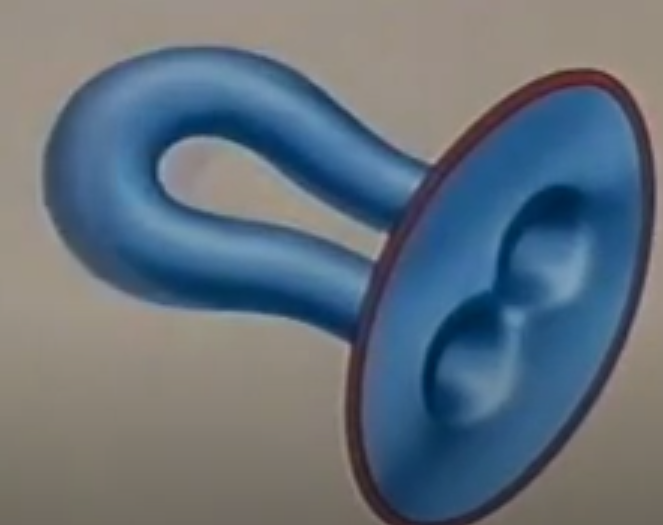
image-20200726214400900

image-20200726214412082

image-20200726214452854

圆环+莫比乌斯带 T # M

image-20200726214509388

圆环+圆盘 L#D = L\D

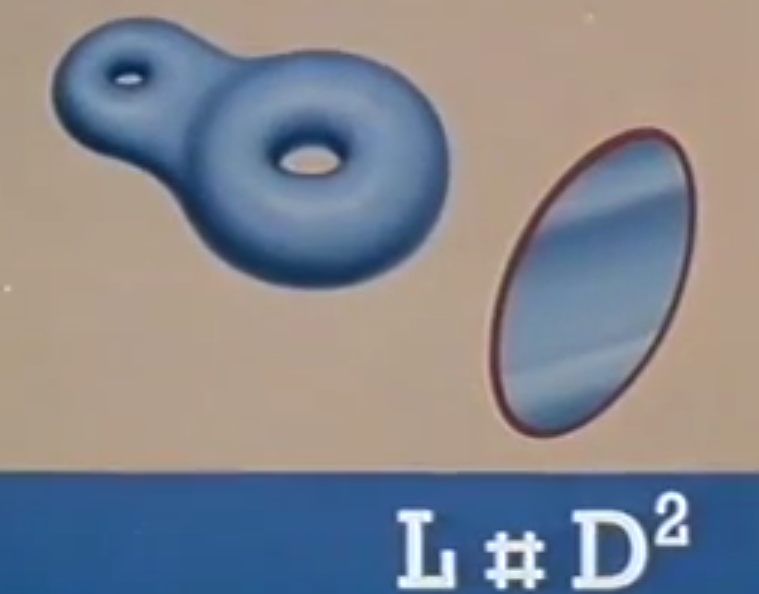
image-20200726215141449

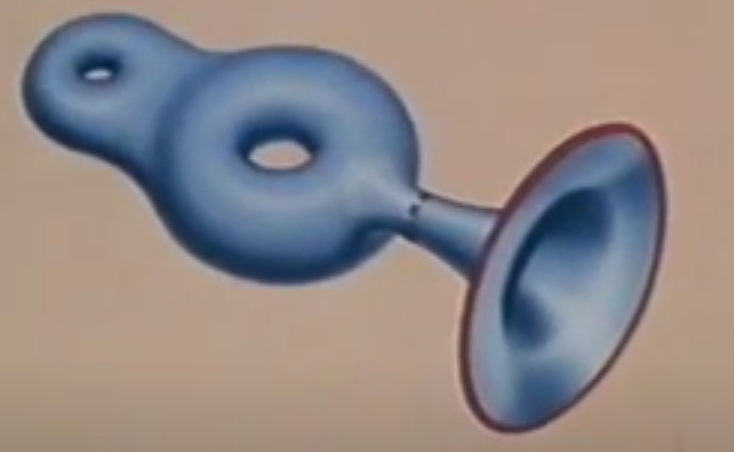
image-20200726215227502

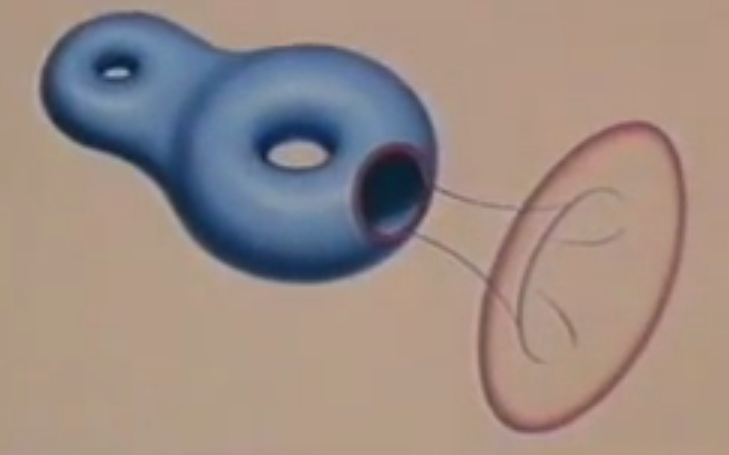
image-20200726215244751

image-20200726215258963

结果相当于圆环减去一个圆盘 L+D=L-D

Youtube一个讲解射影平面的视频

![image-20200726155442814](/images/image-20200726155442814.png)

image-20200726155457405

image-20200726155514917

image-20200726155542389

image-20200726155552526

image-20200726155611749

投影平面=莫比乌斯环U圆盘Disk

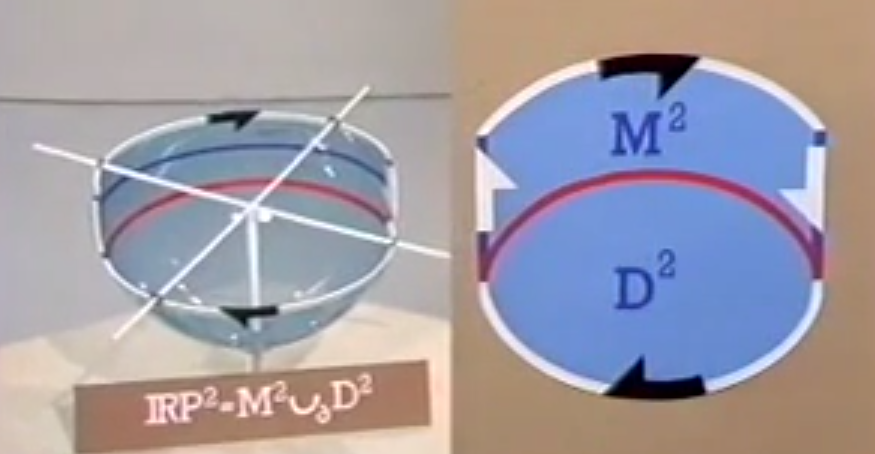
image-20200726155651316

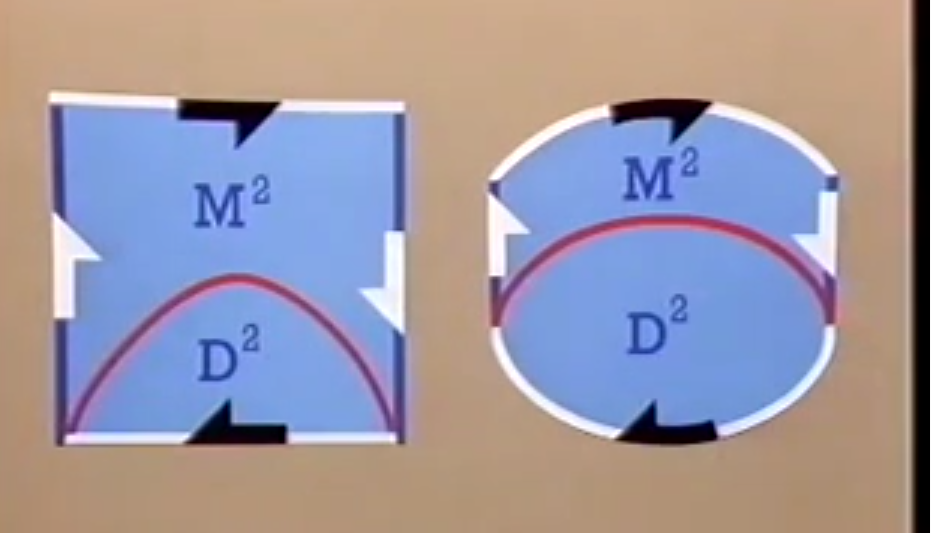
image-20200726155700375

image-20200726155712610

image-20200726155729988

image-20200726155800533

image-20200726155816170

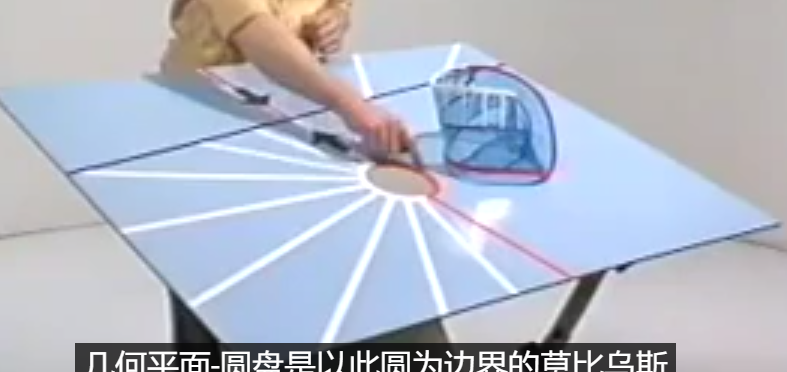
image-20200726155825266

单形与复形

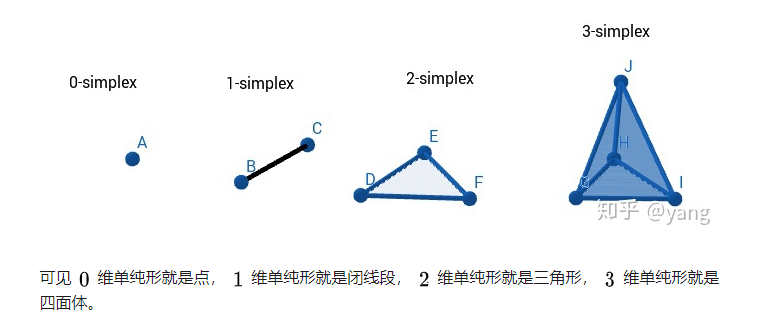
image-20200726160557373

单纯同调群

image-20200726160718926

image-20200726160727215

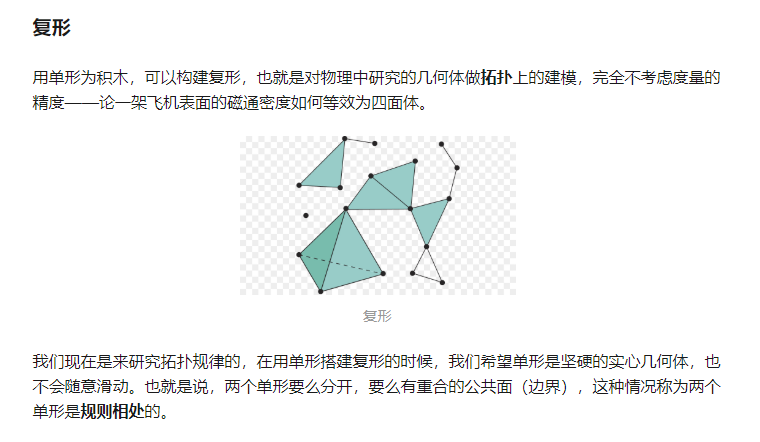
image-20200726160748741

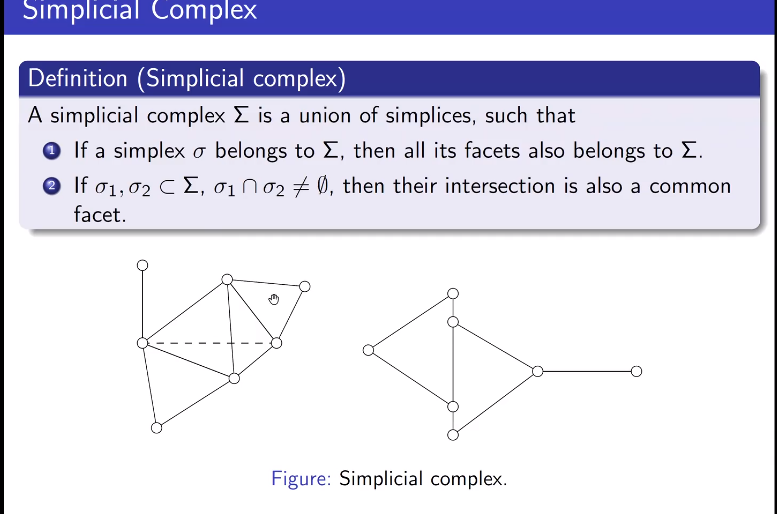
image-20200726160834501

左侧是复形，右侧并非复形，

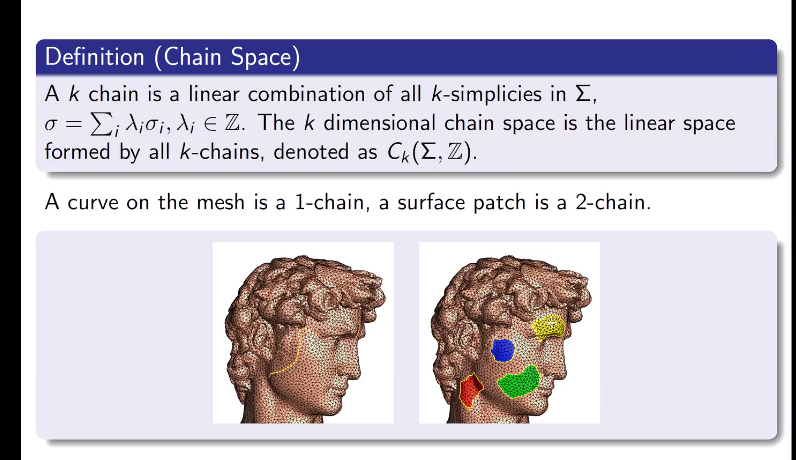
链空间

image-20200726160946059

边界算子

image-20200726161117794

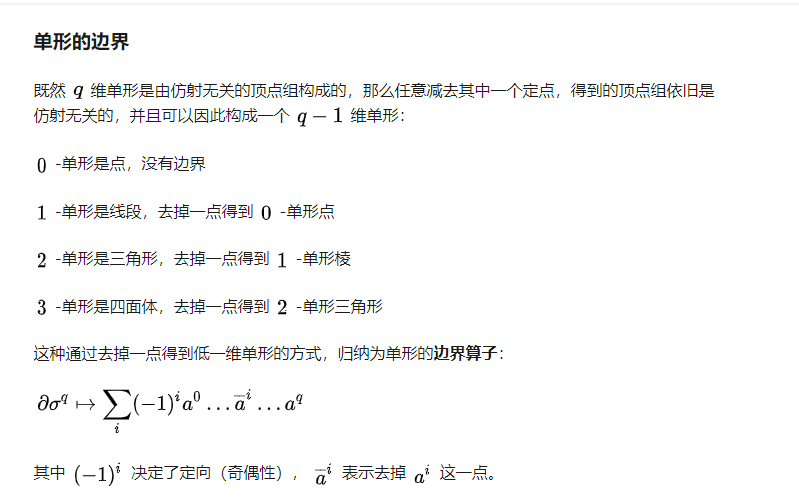
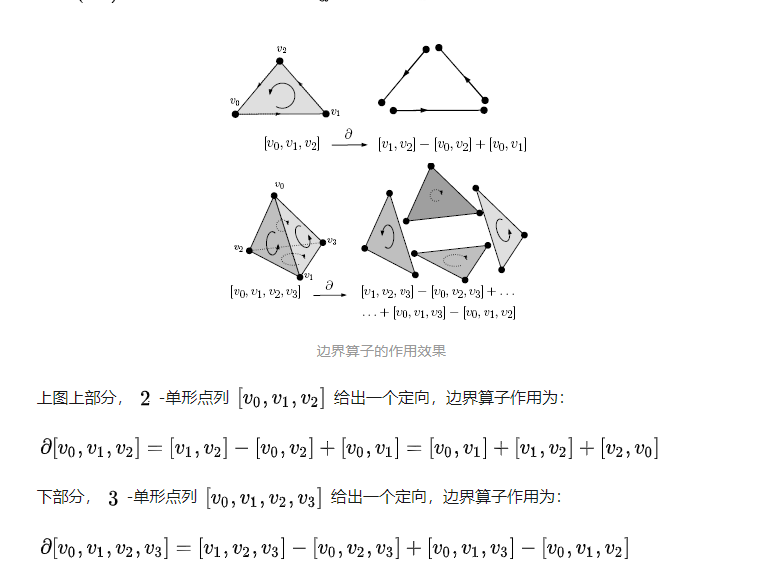
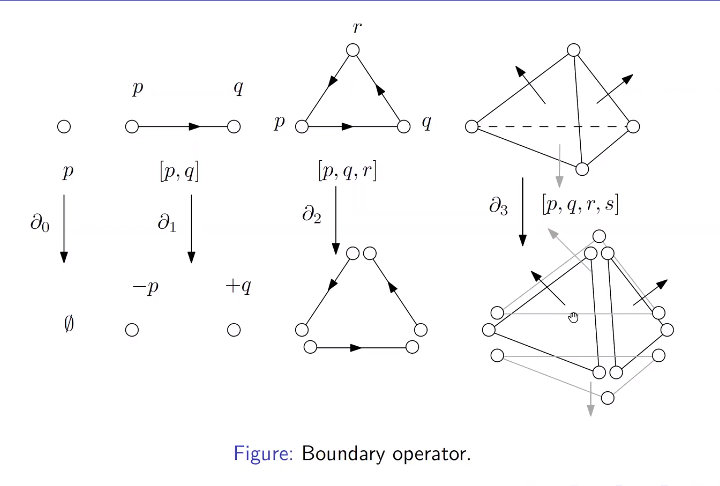
边界算子就像是分解 降维

image-20200727142140492

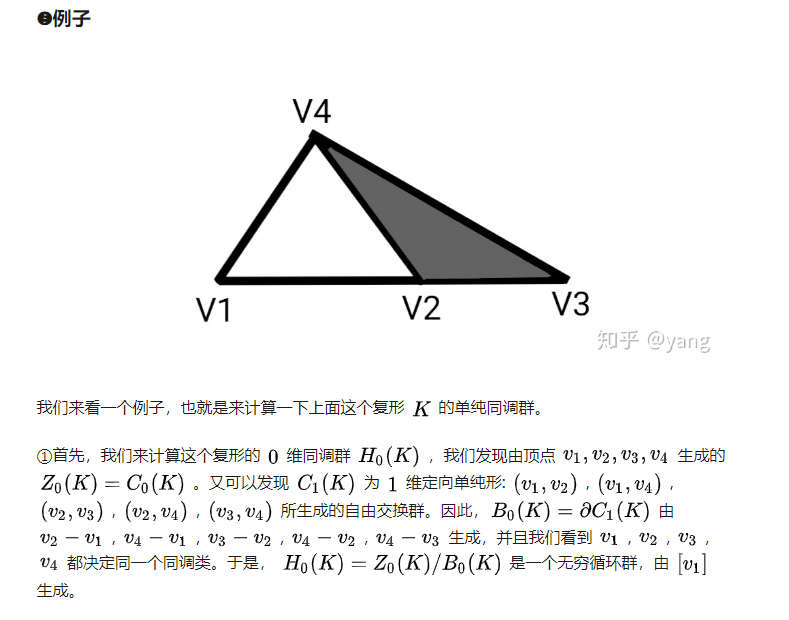
一个边界算子计算的例子

image-20200727142155781

image-20200727142854652

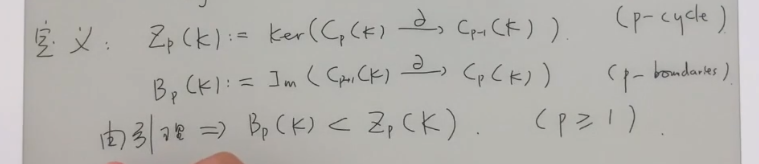
image-20200727143111768

Z 表示圈，B表示边界

image-20200727143302446

image-20200727143448145

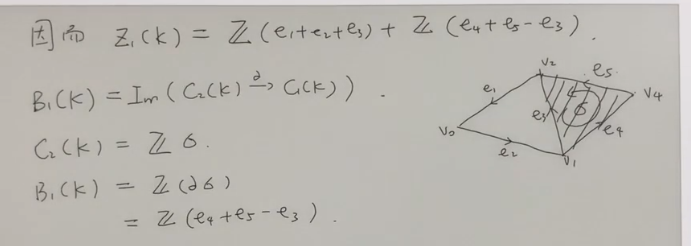
image-20200727150954102

B为实心图形的边界

C为链

image-20200727151039273

闭链

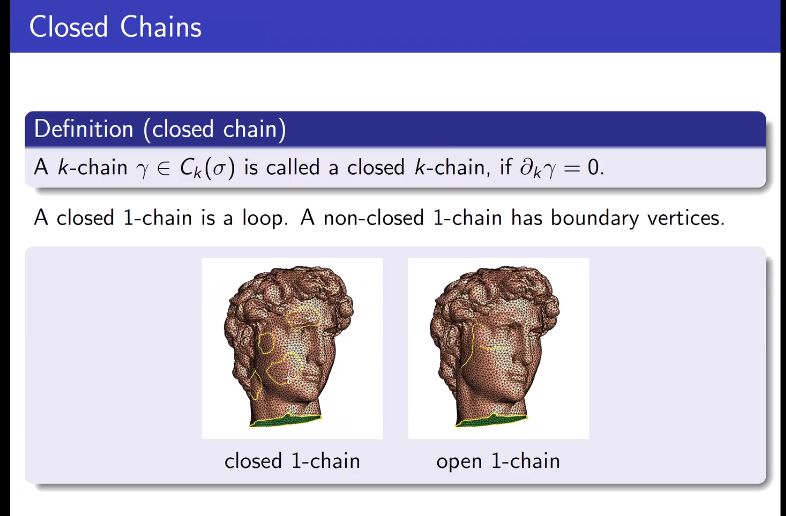
image-20200726161400361

恰当链，边缘链

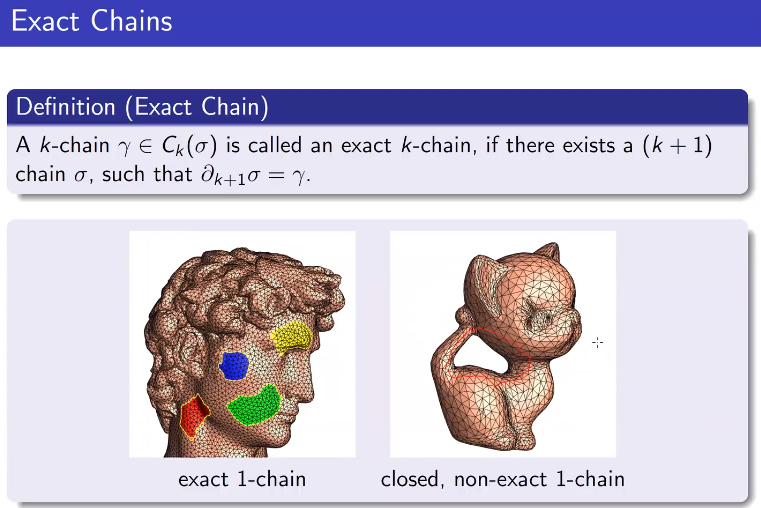
image-20200726161527416

右侧为闭链，但不是恰当链

边的边为空

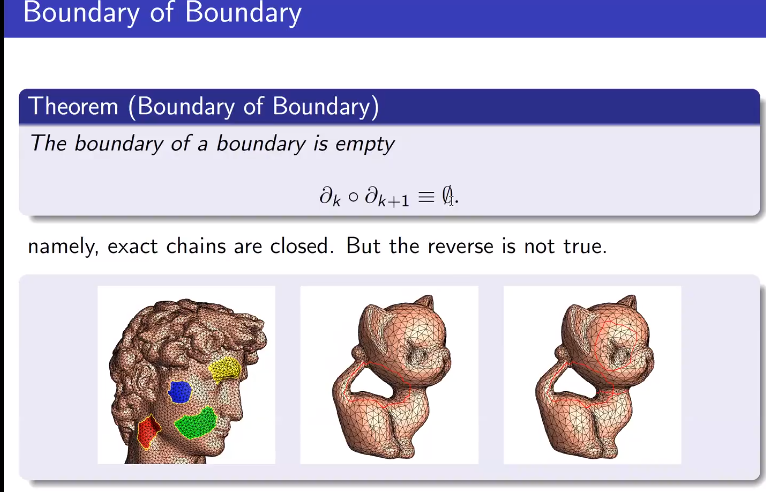
image-20200726161659174

同调群

image-20200726162007885

image-20200726162015676

image-20200727134955577

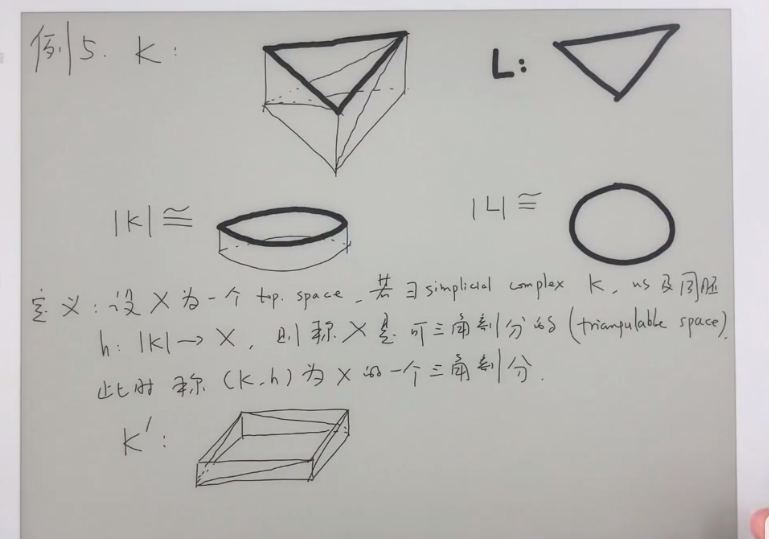
image-20200727135241758

其拓扑空间的三角剖分可以有多个

定向的单形

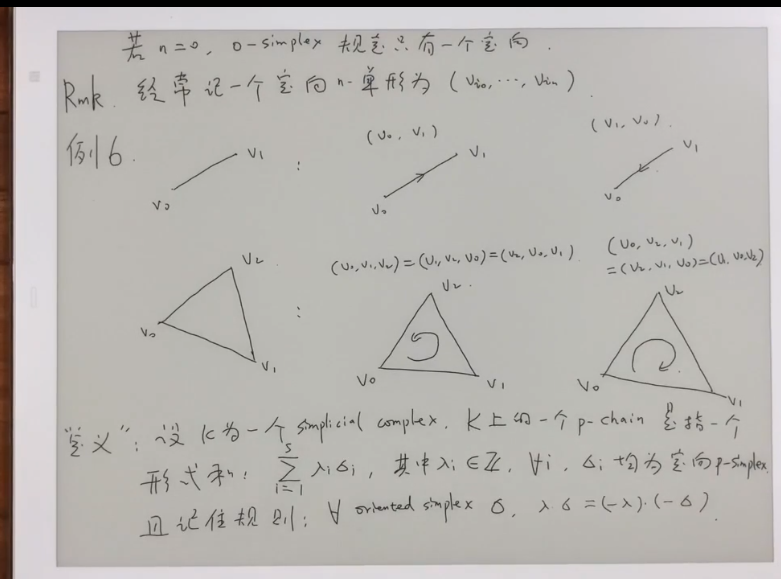
image-20200727135831770

p链等于定向单形的和

image-20200727140152495

C1(K)代表单纯复形的一链

K代表单纯复形

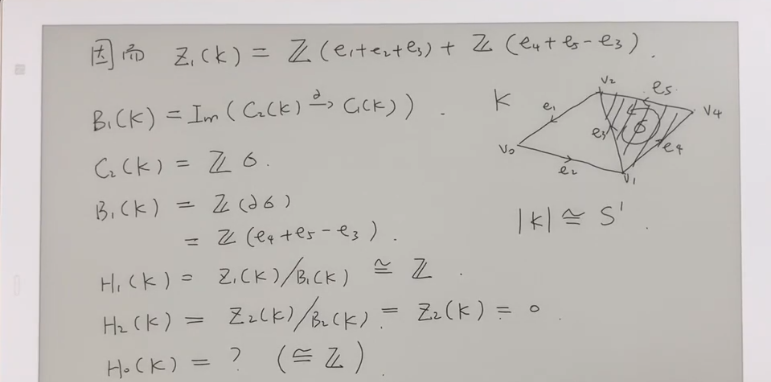
image-20200727151327730

一阶同调群为 一阶圈群/一阶边界群

H(K) = Z/B

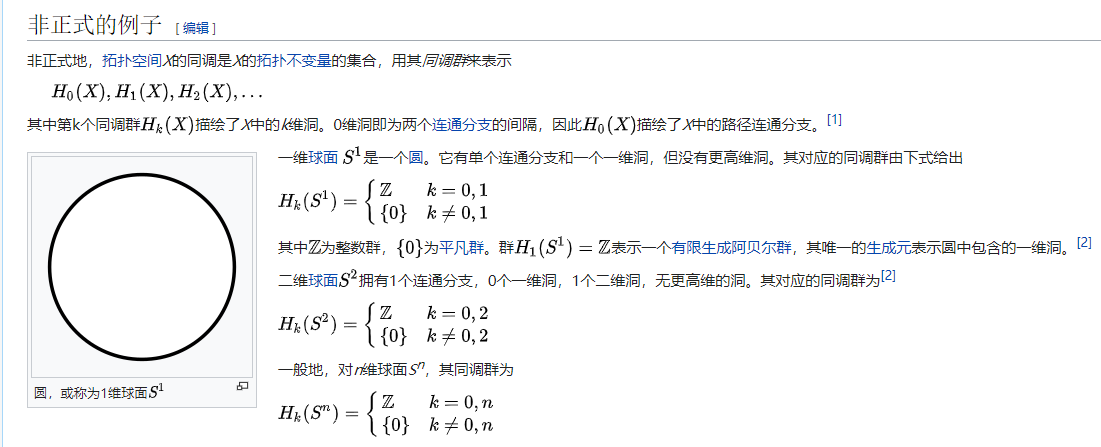
image-20200727151833509

image-20200727151848877

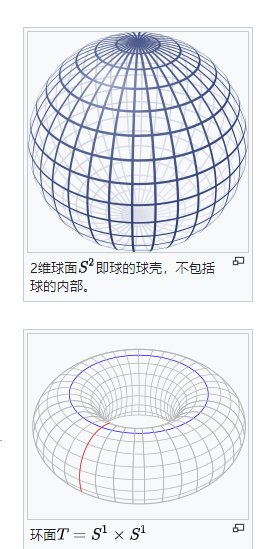
image-20200727151855670

环面同调群的计算过程

image-20200727154132115

image-20200727154556463

image-20200727154930164

image-20200727155229585

image-20200727155359806

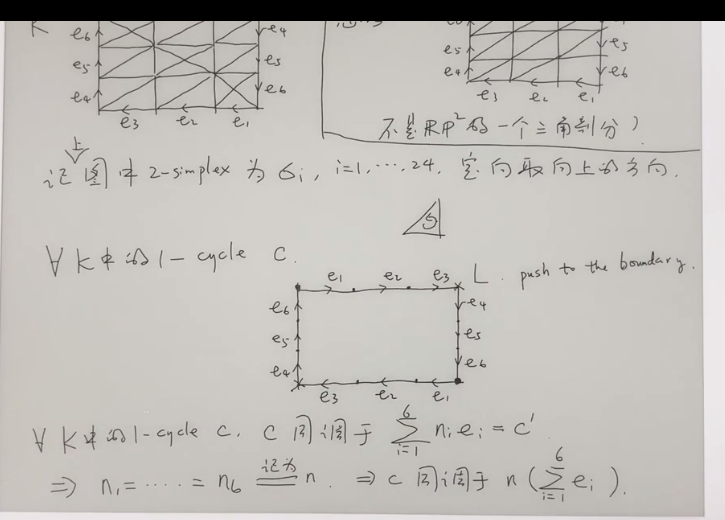
image-20200727175203674

image-20200727175351134

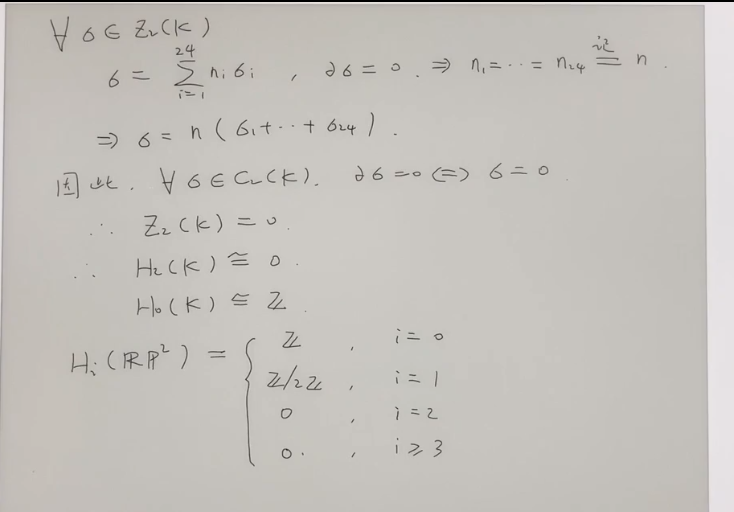
image-20200727175457087

结论:对于一般的拓扑空间，一阶同调群同构与其基本群的abel化

image-20200727175626648

单纯同调群

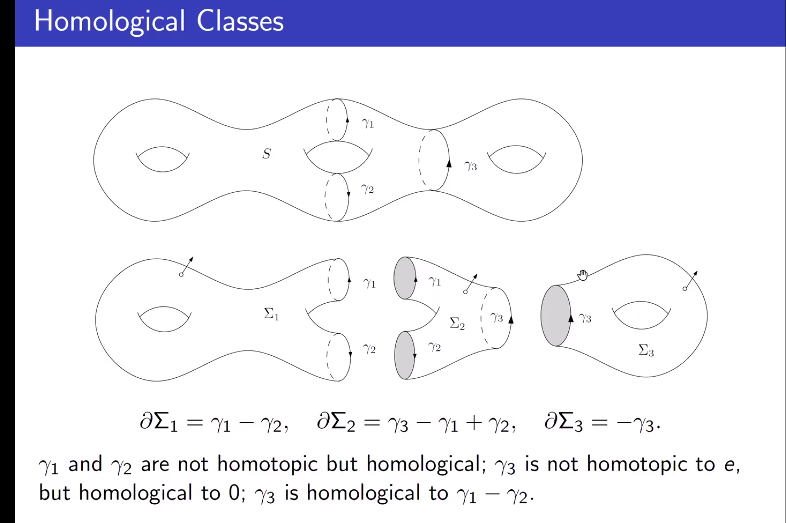
image-20200726162602425

上同调群与上链空间

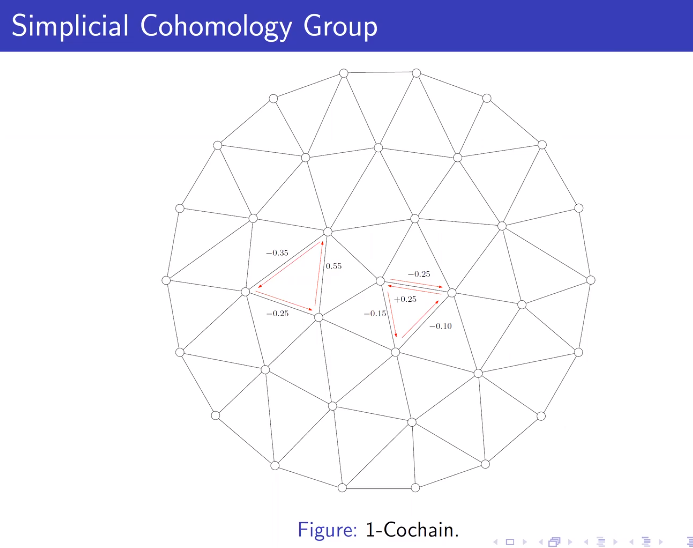
image-20200726163557458

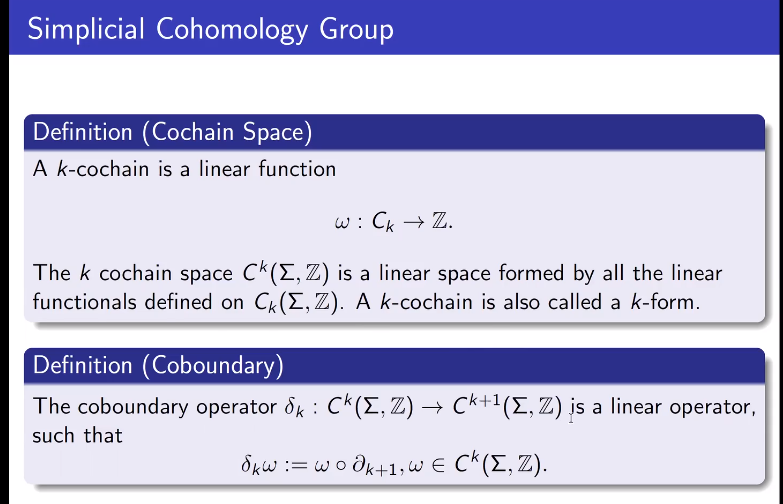
image-20200726163650680

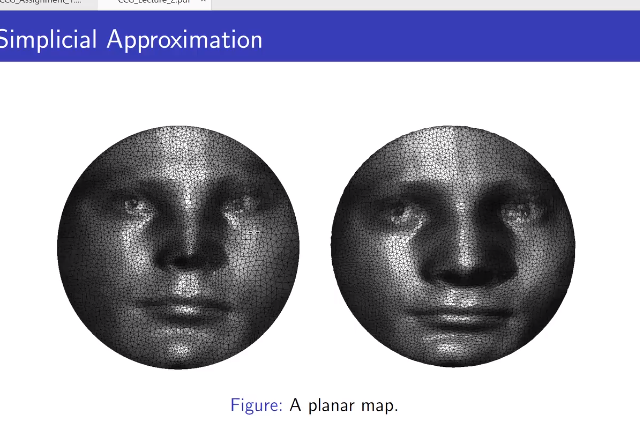
单纯映射

image-20200726165536675

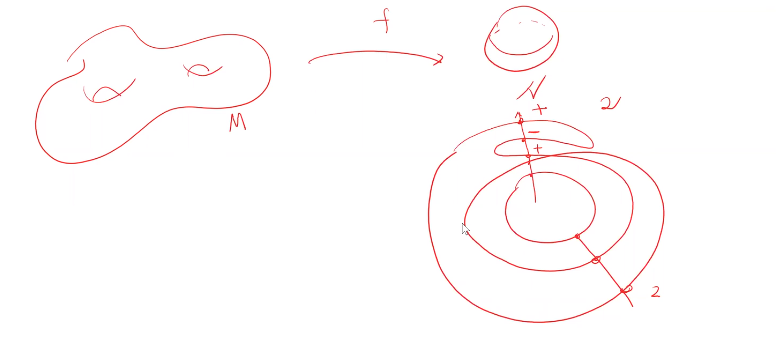
映射度

image-20200726170212704

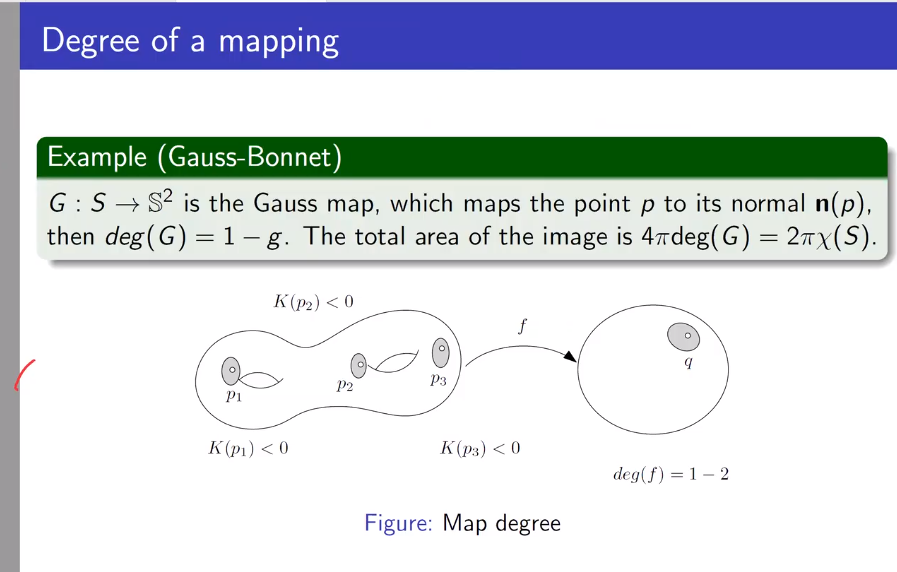
image-20200726171323106

高斯映射

参考

同调维基百科

Simplicial homology Wiki

单纯同调群 zhihu

单纯同调群 baike

计算共形几何讲义 （4）单纯同调

[轻松愉快] 拓扑学 Topology & Geometry by Dr Tadashi Tokieda

射影平面 维基百科 射影平面 百度百科 real projective plane 实射影平面 wiki

映射的度

Orientable and Nonorientable Surfaces

The Fundamental Group of the Real Projective Plane

Real projective plane and Moebius strip

Numberphile youtube

Topology Riddles | Infinite Series

Real Projective Plane-Connected sum

The Klein bottle

Projective plane: a history

The Real Projective Plane youtube anime

The Möbius band and the projective plane youtube anime

欢迎关注我的其它发布渠道