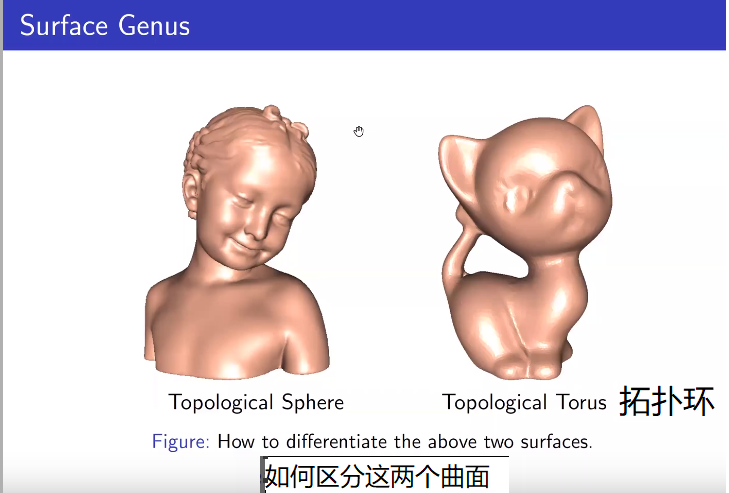
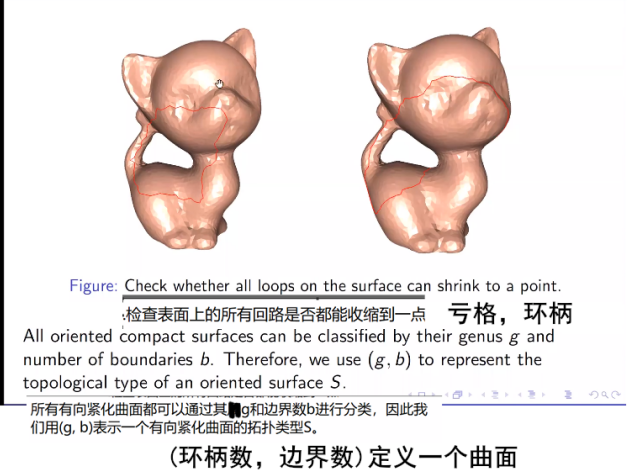
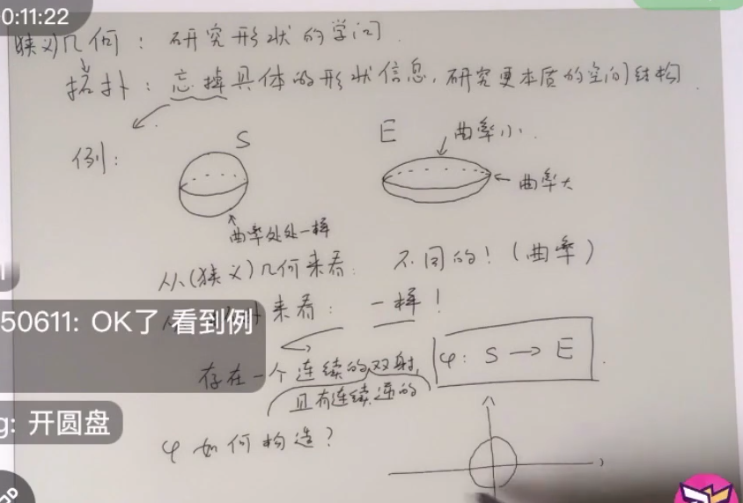
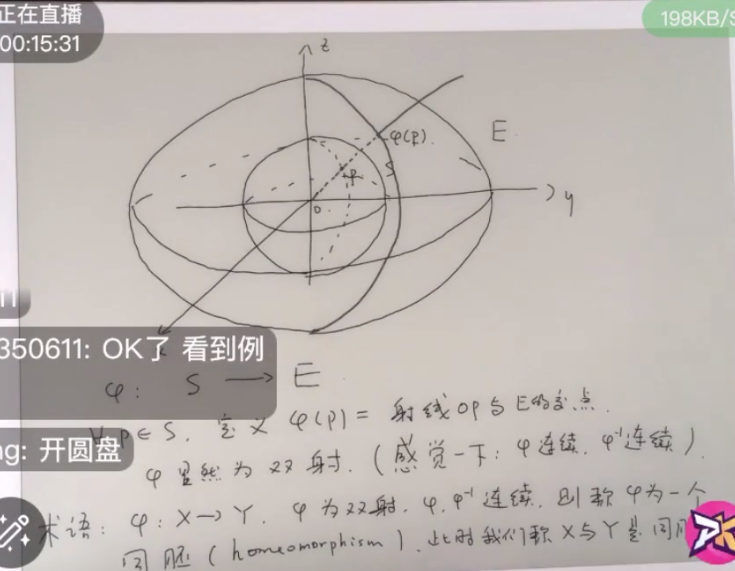
如何定义一个曲面
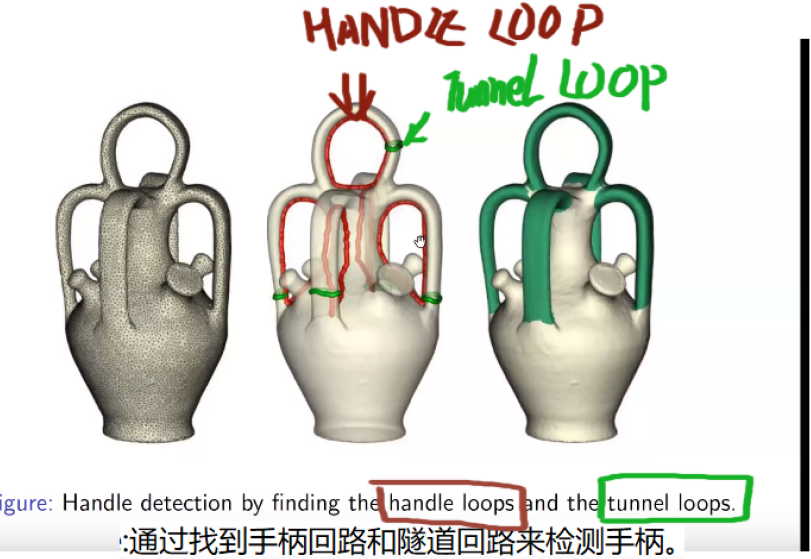
Handle loops 在外部缩成一个点,t unnel在内部缩成一个点。
环柄在医学上的应用
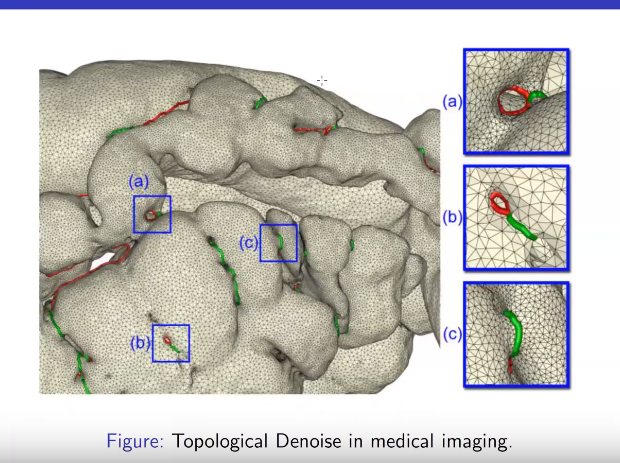
拓扑去噪,用环柄找出大肠微小的环柄,一些医疗设备,西门子会使用这些技术。
代数拓扑与群

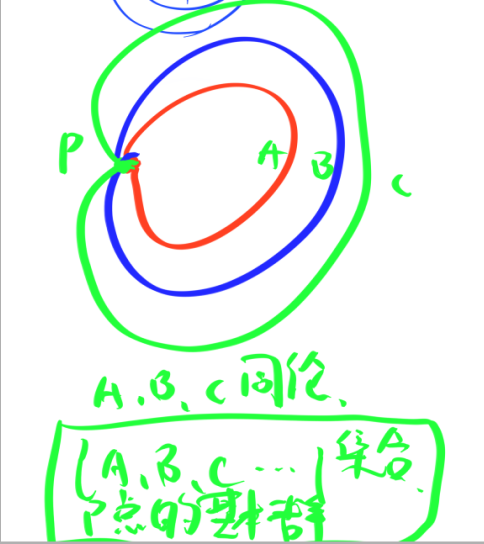
1.基本群的定义


所有过基点的环路集合
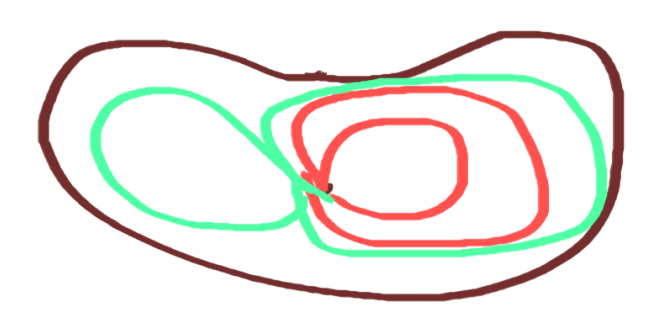
这样?环路的同伦类好像还是在这个集合里?
2.何为同伦
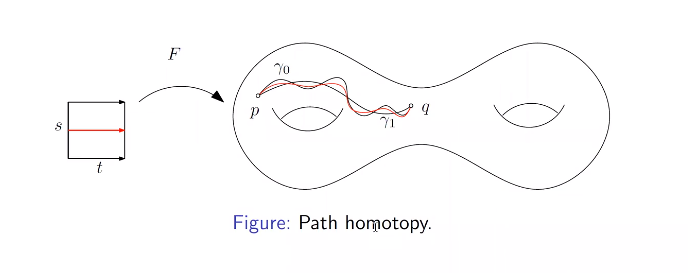

同伦是一种等价关系

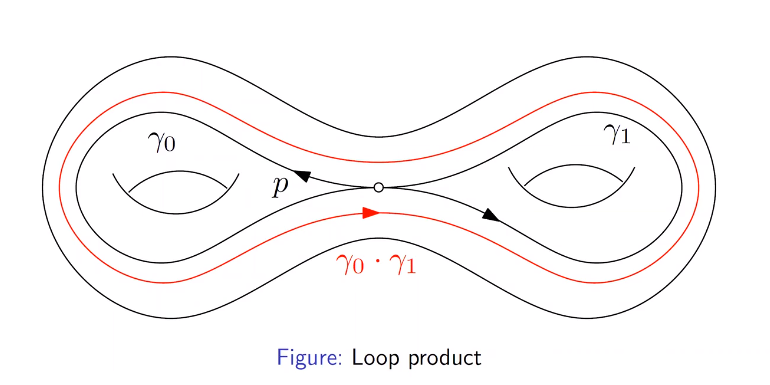
3.乘积和逆
环路的乘积

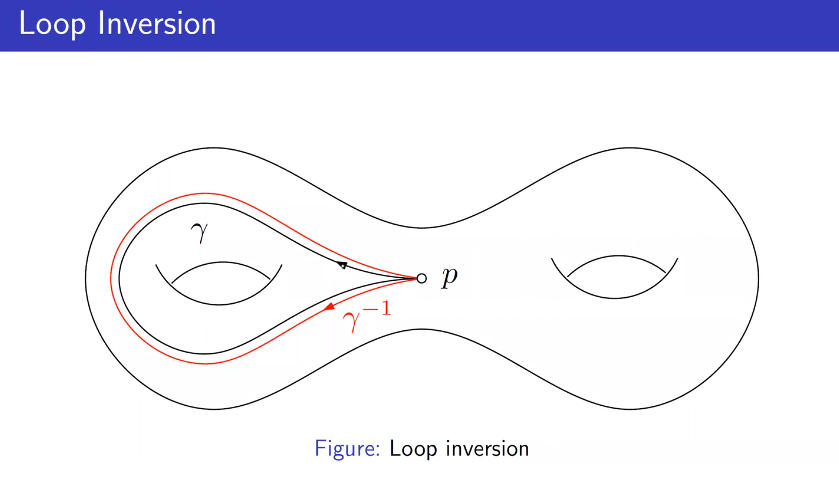
环路的逆
基本群的表示

使用字母来表示环路
词群的插入和删除操作


曲面交叉索引的值,交点曲线切向量叉积和法线同个方向值为1,垂直值为0,相反为-1,这样为每个焦点定义了一个指标。
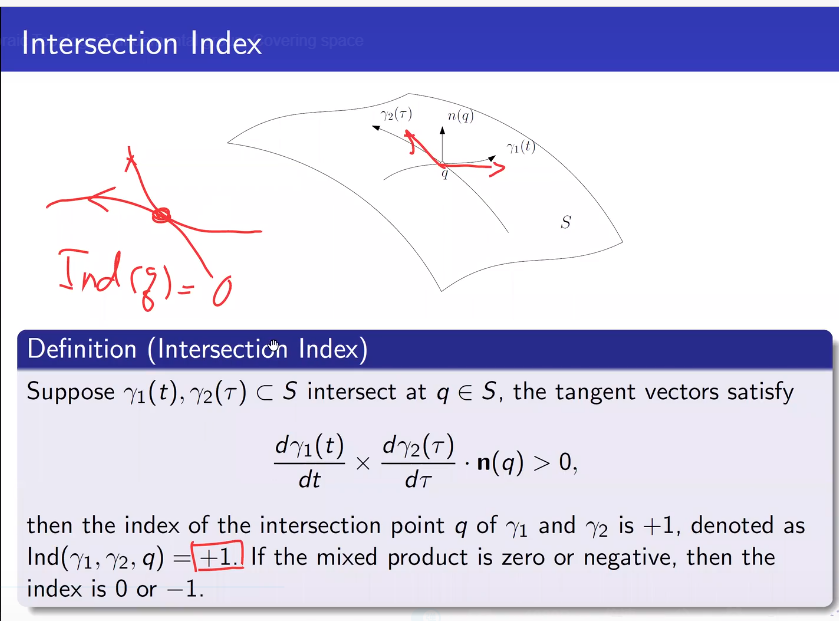
代数相交数


代数相交数在同伦变换下不变
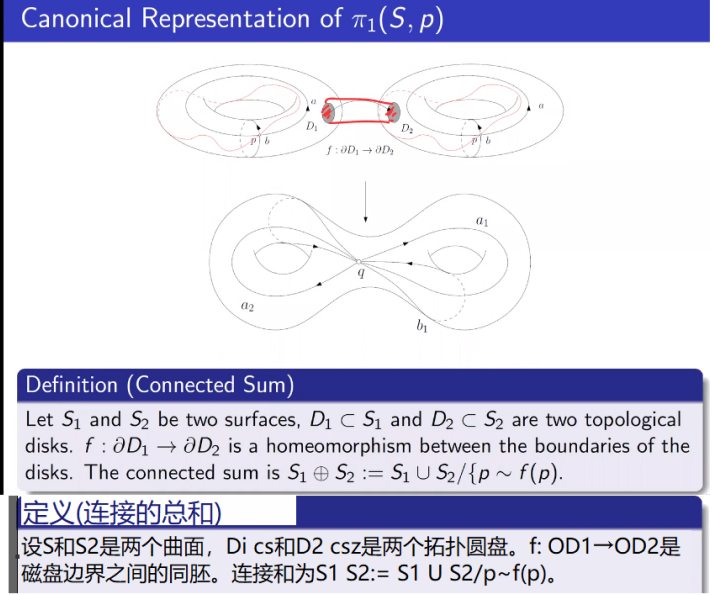
基本群的典范表示


a1,b2,a2,b2 叫做曲面基本群的典范基底。
拓扑同胚和基本群(Homeomorphism)

两个曲面的基本群同构,则其拓扑等价,即拓扑同胚。


莫比乌斯环是不可定向的曲面

球和圆环是可定向的曲面

曲面不可定向则包含莫比乌斯环,包含莫比乌斯环的曲面必然不可定向

没有边界并且不可定向的曲面
基本群的概念和正交基之类的相同(应该),即使用最少的元素表示一个空间或者曲面。
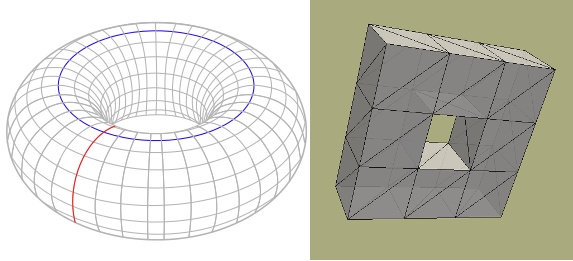

拓扑空间分解

曲面的连通和
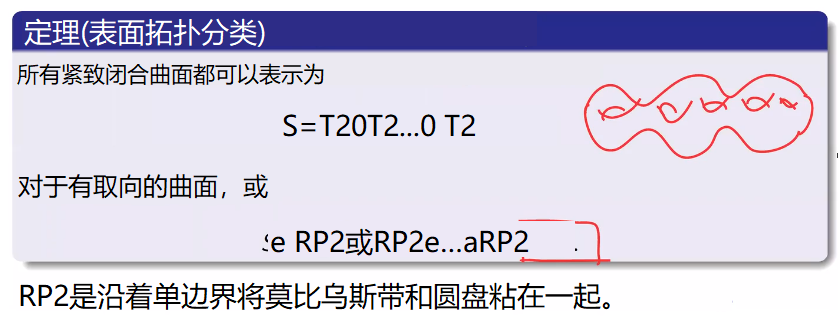
表面拓扑分类

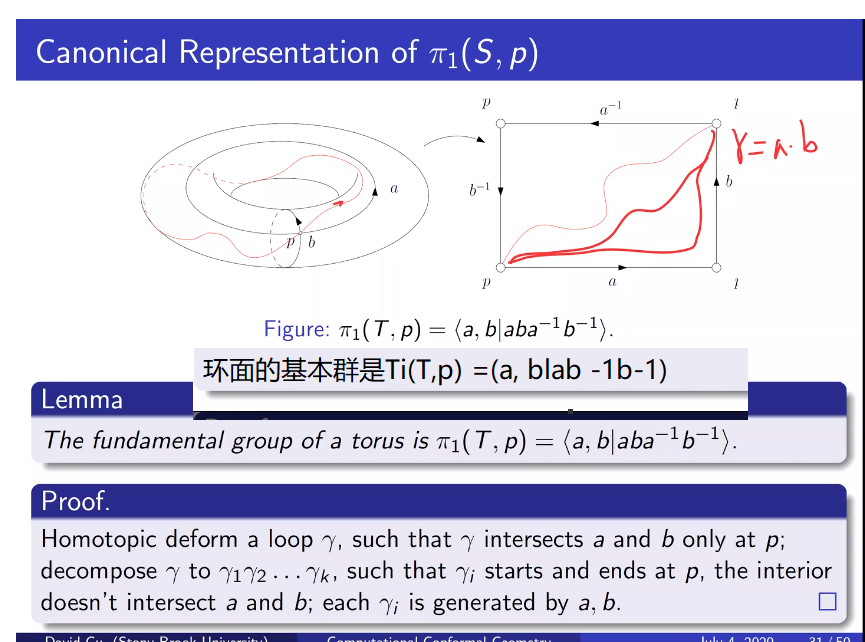
环面的基本群
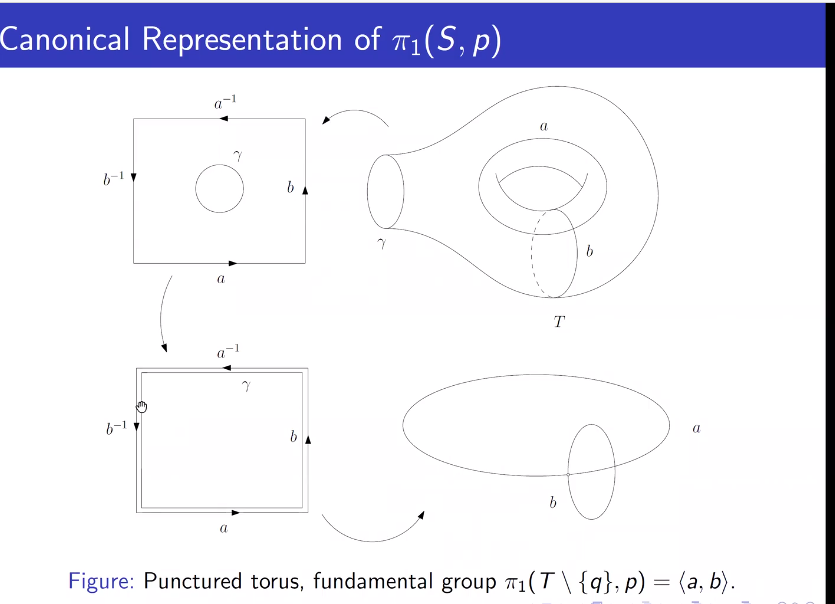
刺破环面基本群的表示(亏格为2的曲面的基本群表示)
其证明


切图(Cut Graph)
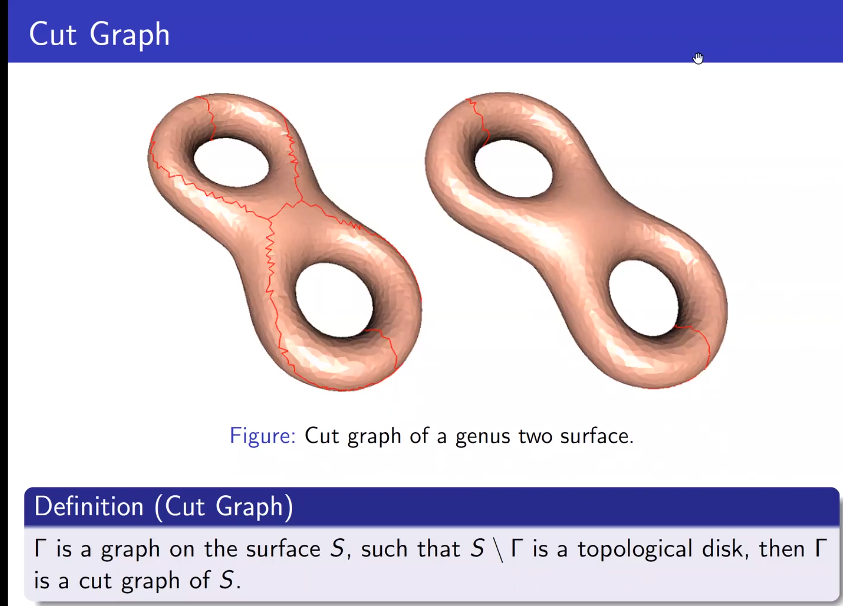
计算切图的算法

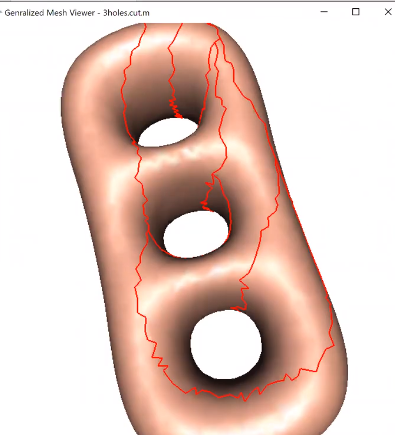
亏格为3的切图

基本群的关系算法
万有覆盖空间(?)

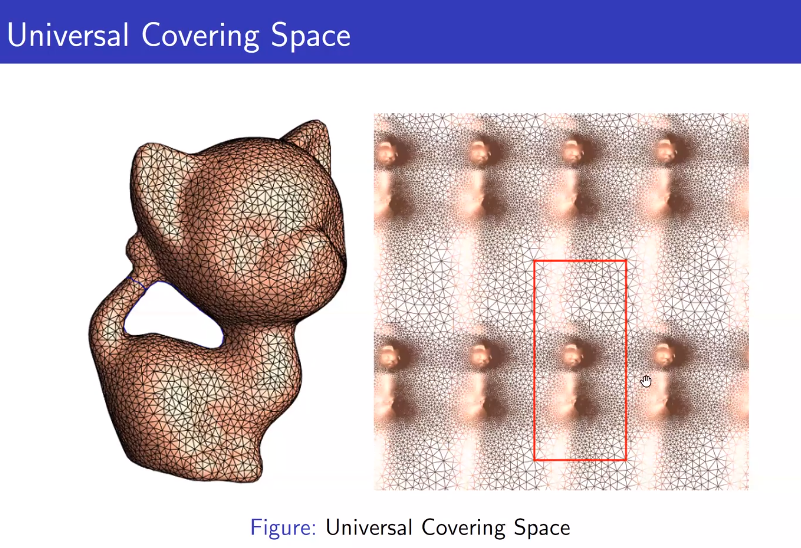

覆盖群的结构

亏格为2的曲面的万有覆盖空间
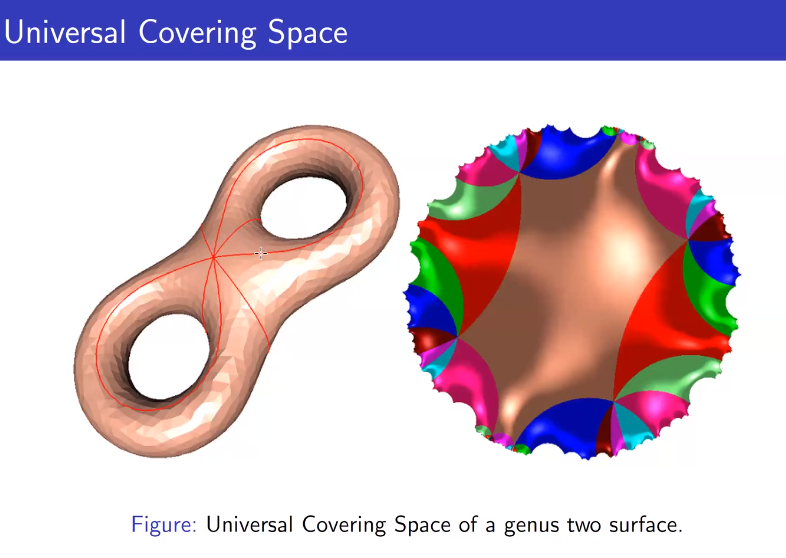

万有覆盖空间的算法表示

基本拓扑学笔记
第一节:欧拉定理
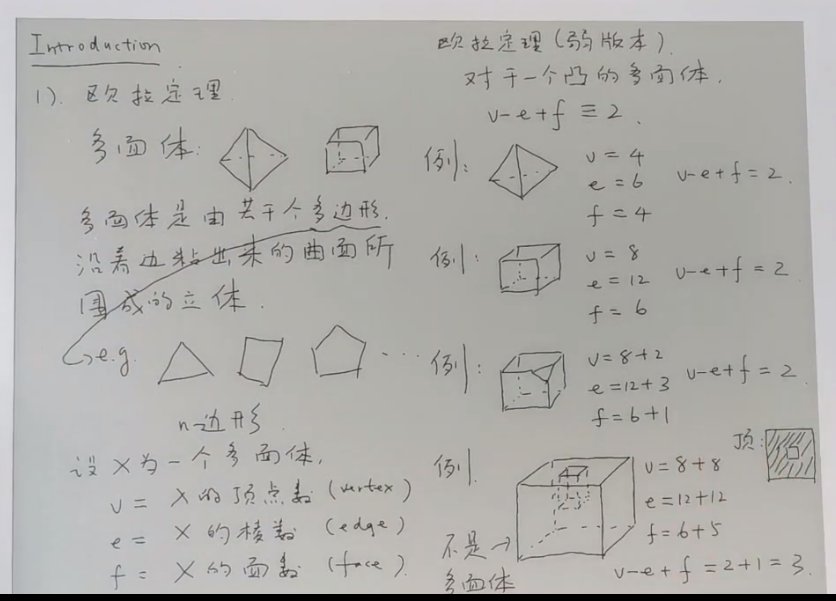
1.欧拉定理

凸多面体的任何截面都是凸多边形,与凹多面体相反。
把凸多面体的任何一个面伸展成平面,它的所有其他各面都在这个平面的同侧。
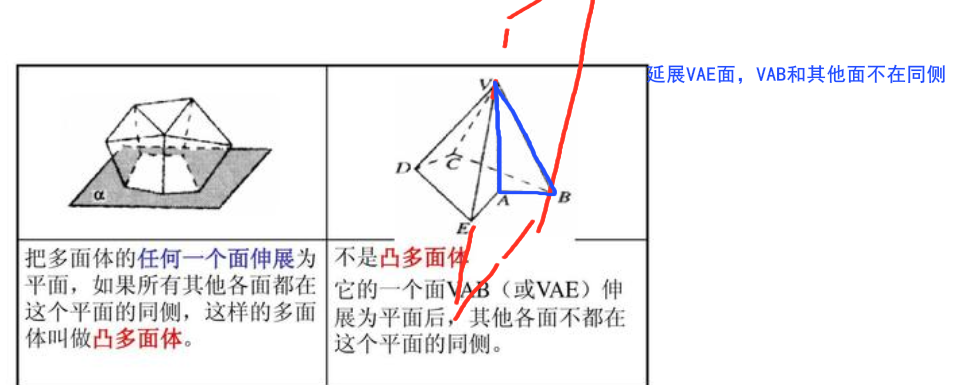
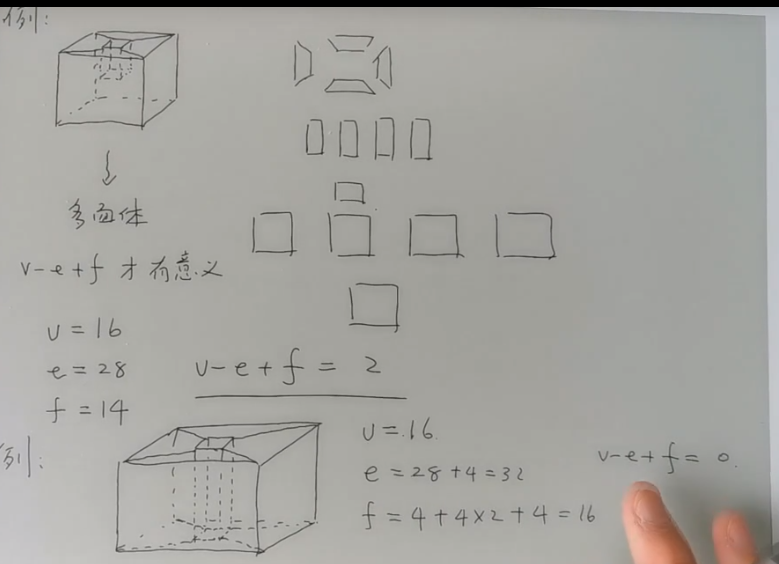
最后一个计算没有意义因为顶面的形状不算是多边形。
v-e+f=0的例子
几个多面体其本质的不同
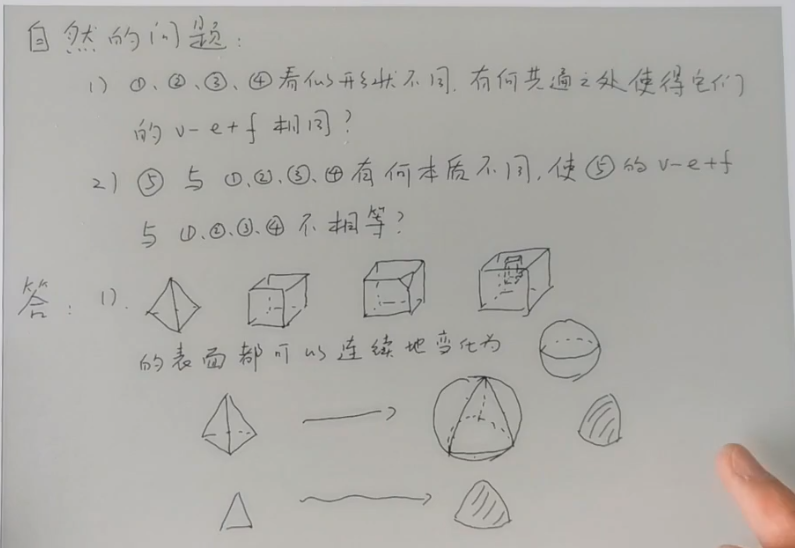
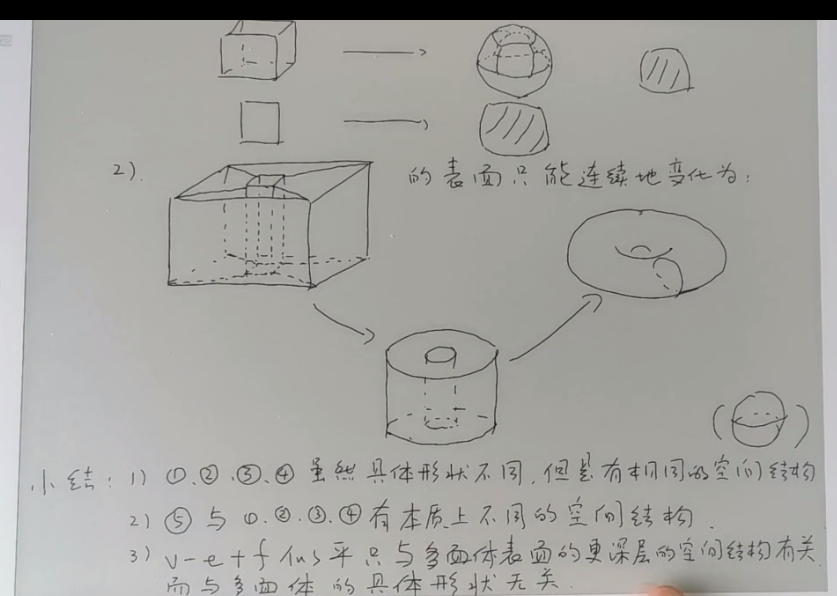
具体的几何形状无关,而更深层的几何结构有关
第二节:拓扑引论
同胚
双射
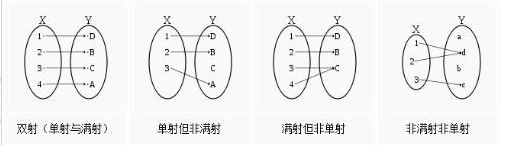
不同胚的例子
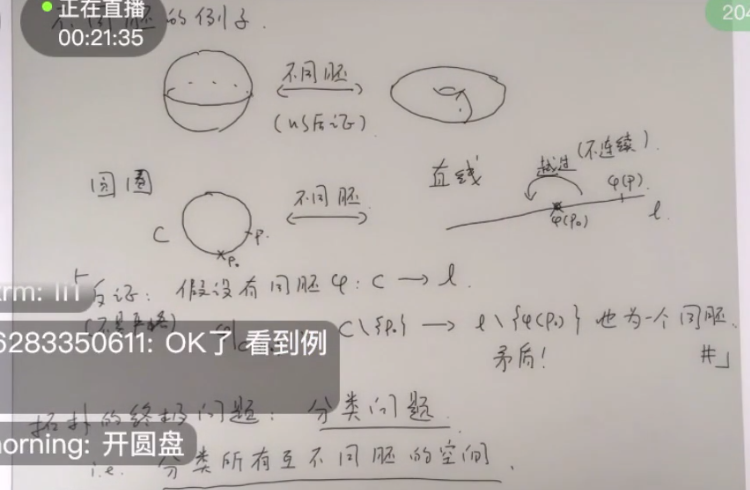
拓扑不变量

什么是连续
微积分中的连续定义

开集与逆


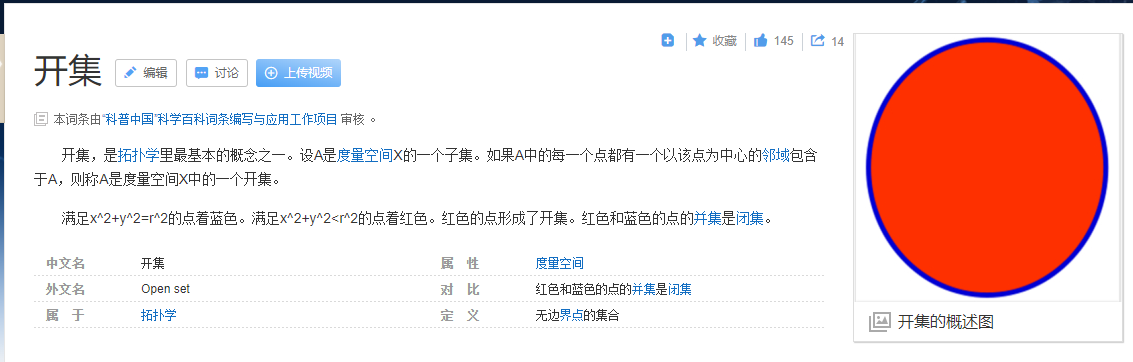

第三节:拓扑空间

有限个开集的交为开集
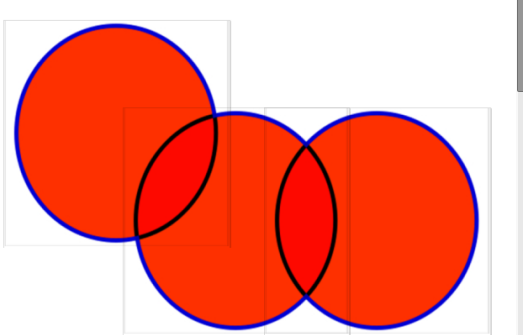
这样?
平凡拓扑 只有空集和全集
离散拓扑

度量空间

度量空间(metric space)是一种具有度量函数(metric function)或者叫做距离函数(distance function)的集合,此函数定义集合内所有元素间的距离,被称为集合上的metric。
度量空间中最符合直观理解的是三维欧氏空间,事实上,metric的概念是欧氏距离性质的推广。
度量空间是1906年Maurice Fréchet在其著作中引入的,但是名字来自于Felix Hausdorff。
度量空间在分析学中有重要应用。
实数序列的极限与metric function



除了极限的概念,通过度量空间还可以定义连续、一致连续、Lipschitz连续、一致收敛等性质,度量空间本身还可以具有很多性质,如完备性、紧致性、连通性、分离性等。此外度量空间还能导出开集与闭集等拓扑性质,这导致了对再度抽象的拓扑空间的研究。
数学是一个不断抽象的过程,度量空间以及更加抽象的拓扑空间的引入,并不是为了抽象而抽象,而是为了研究的方便,使概念准确和简洁。
度量空间诱导的拓扑
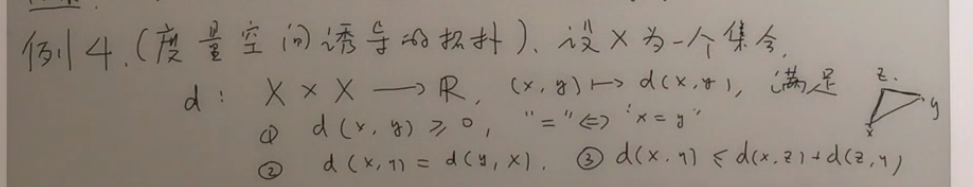
子空间拓扑

