如何制作一张地图?

怎么样做一个地球的平面图?很难,就像把橘子皮摊平一样,如果没有扭曲和切割几乎不可能。
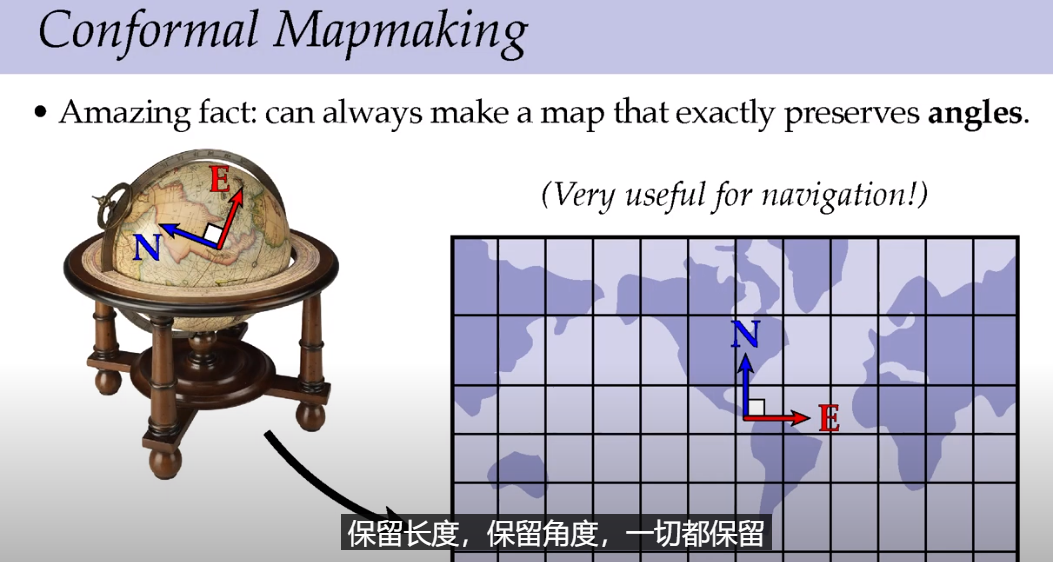
既然不能尺寸和角度不能都保留,那么共形几何选择在绘制地图的时候保持角度,在航海地图的时候很有用。
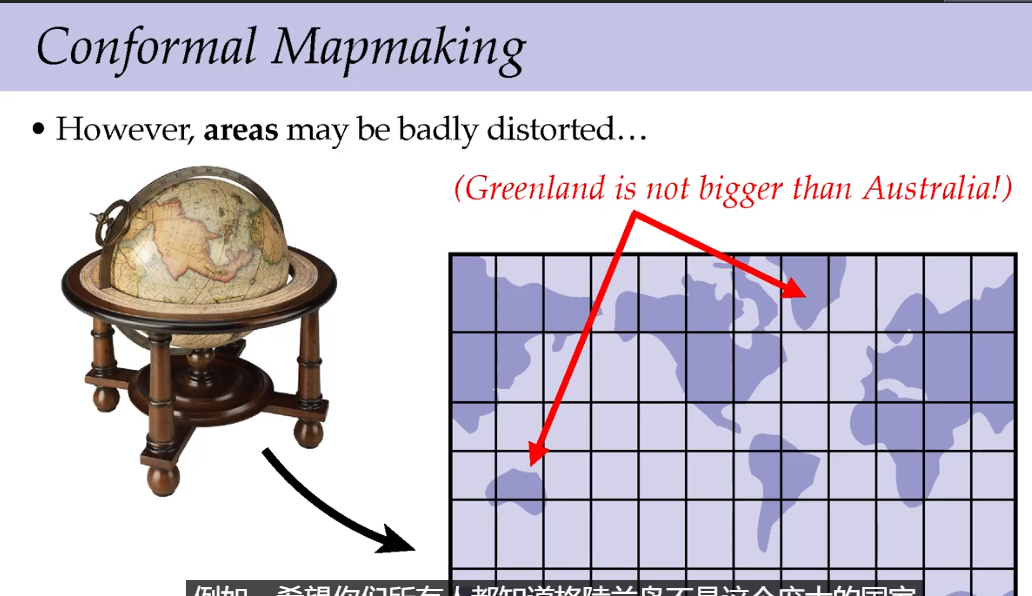
保留角度会使得地图上一些区域的面积严重扭曲,例如在地图上看,格陵兰岛面积比澳大利亚大,但是实际上澳大利亚面积768万平方千米,是世界上最小的大陆;格陵兰岛面积216万平方千米,是世界上最大的岛屿。澳大利亚的实际面积相当于格陵兰岛的三倍多。
经过将球体地图投影到平面上,角度得到了保留,但是局部的尺寸和比例发生了严重的变化。

一般来讲,共型几何研究的是保持角度。


为何保持角度?
那为什么要保持角度不变,即共形?

计算效率和几何处理效率更高。
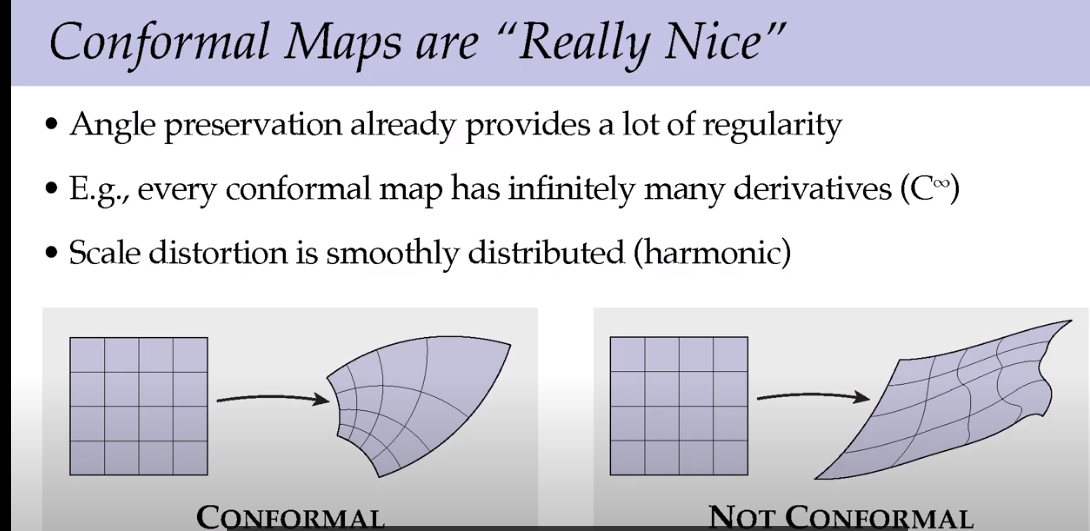
尺寸变化非常平滑。

假设在地球上旅行,可以不用思考角度问题,而只考虑尺寸,这样简化了问题。
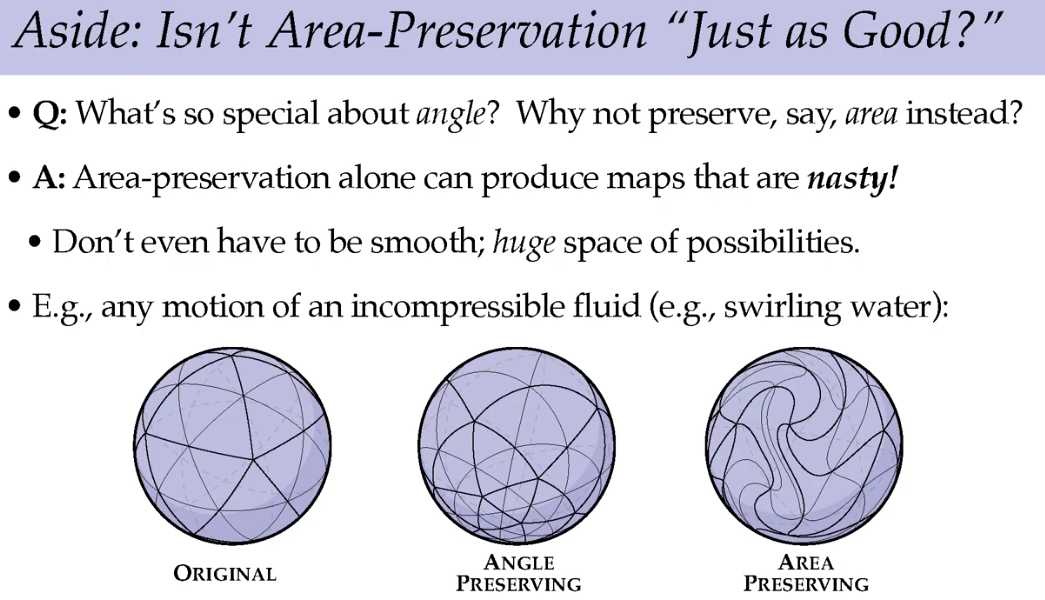
那为什么不保留面积?保留面积产生的图形极为复杂难懂,也不平滑。
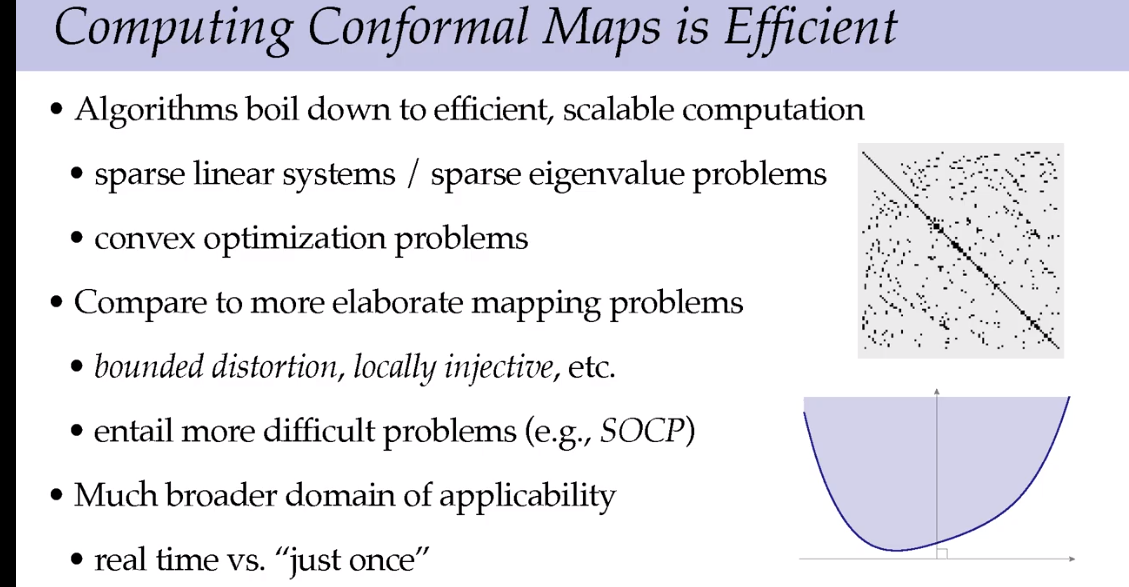
共形几何可以解决很多问题。
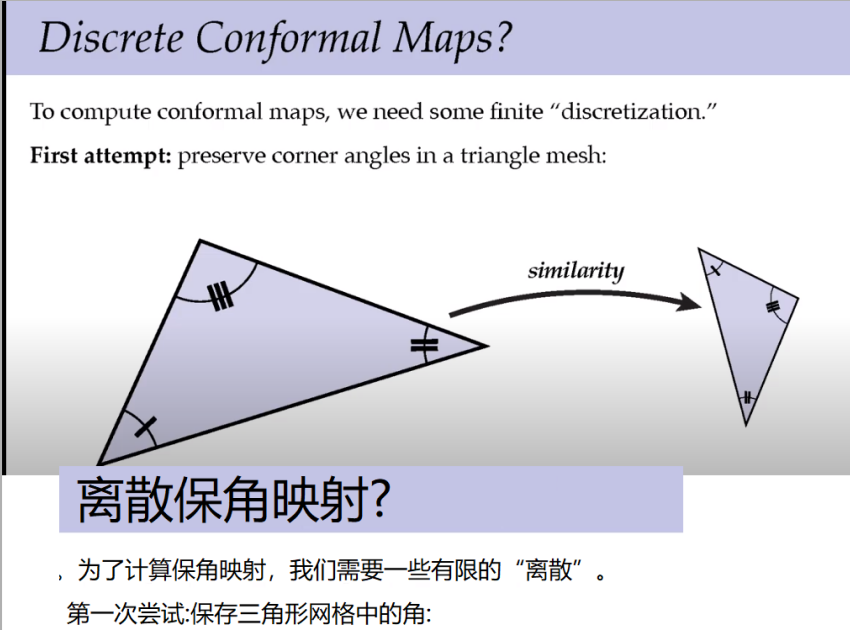
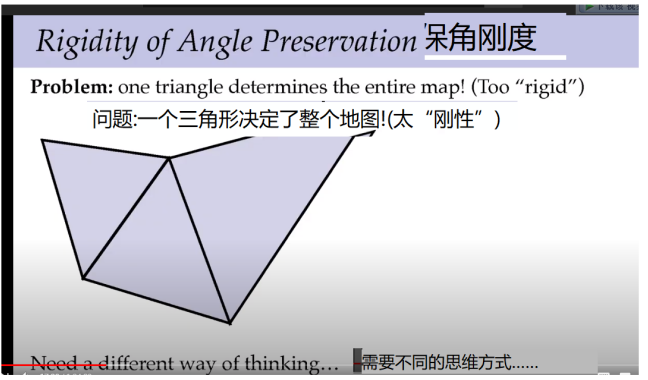
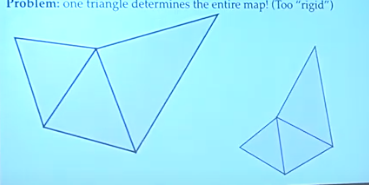
一旦把第一个三角形保留了角度,其他的都不能变了。结果已经固定,这时候需要一些别的思考方式。
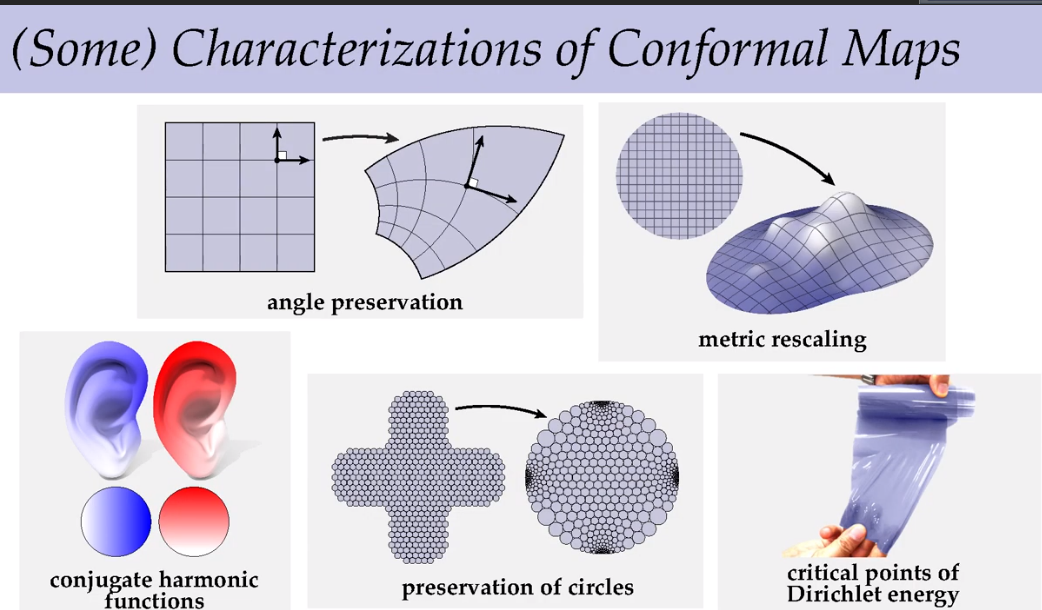
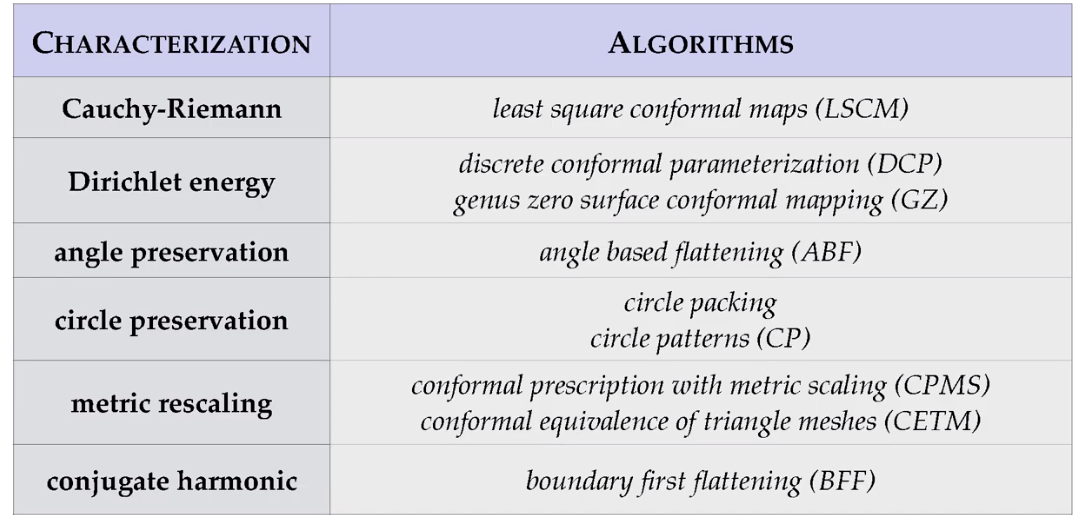

曲面的保角映射
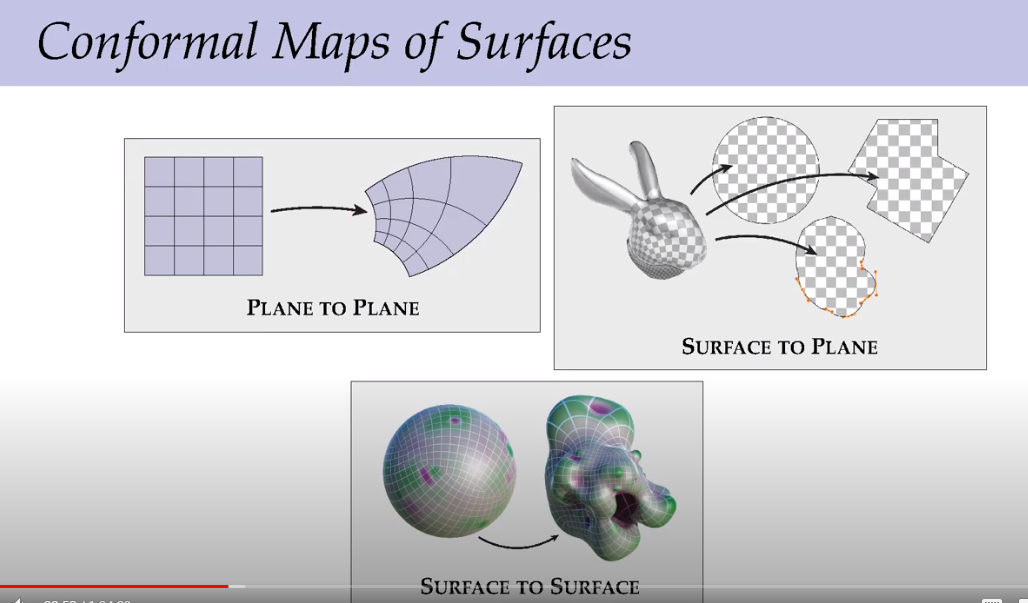

把雕像展为2维平面和制作一幅地图的过程是一样的。
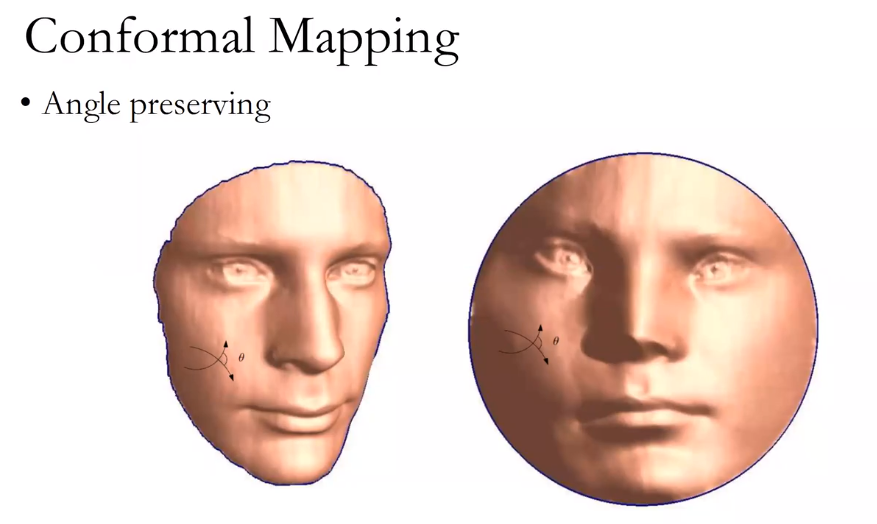

如果在平面上绘制小圆,则经过变换之后的3维空间中的圆形则会保持角度,但大小会发生扭曲,变成椭圆。
共形映射补充(2020-11-8)
来源:复变函数与积分变换 华中科技大学 MOOC 尹慧 第六章共形映射

伸缩率的概念

旋转角的概念

导数的几何意义

我TM直接爆炸草?
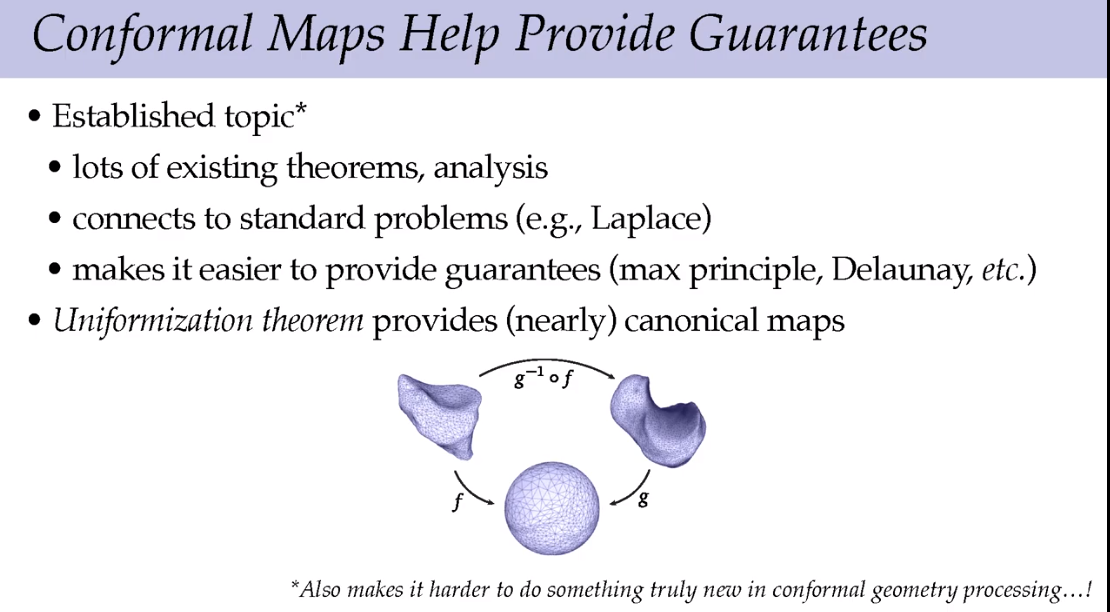
单值化定理
所有带度量的封闭曲面都可以共形映射到三种标准空间中的一种,球面,欧式平面或者双曲球面。
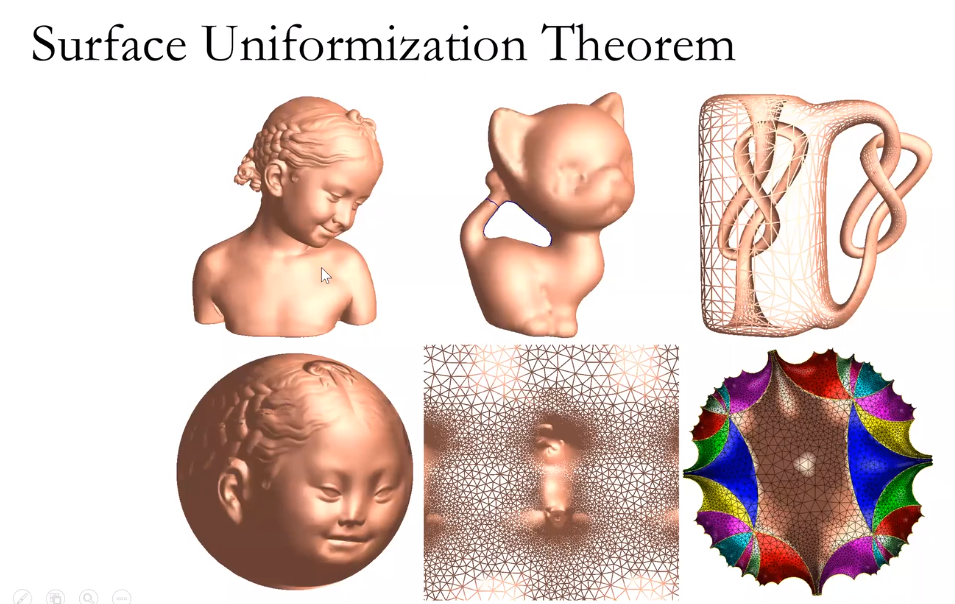

0亏格的封闭曲面保角变换到球面上。

亏格为一的曲面映射到欧式平面上。
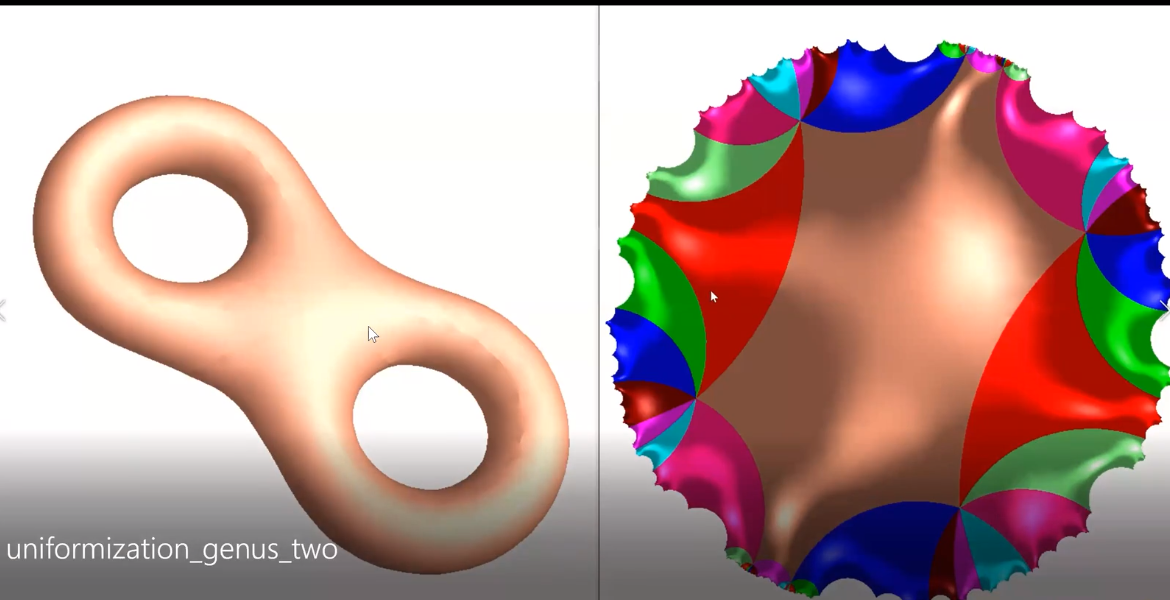
亏格为2的曲面覆盖整个双曲曲面。
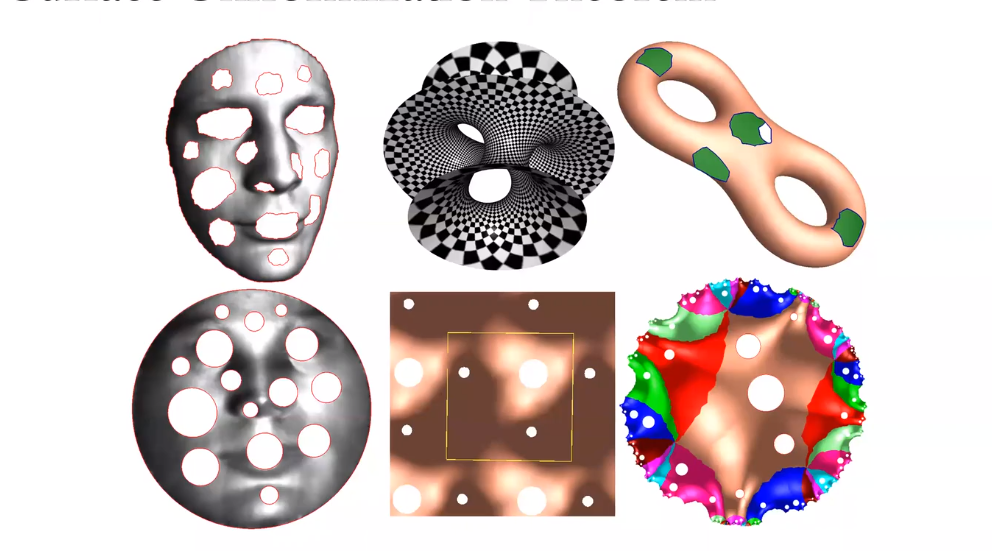
带有边界的曲面。
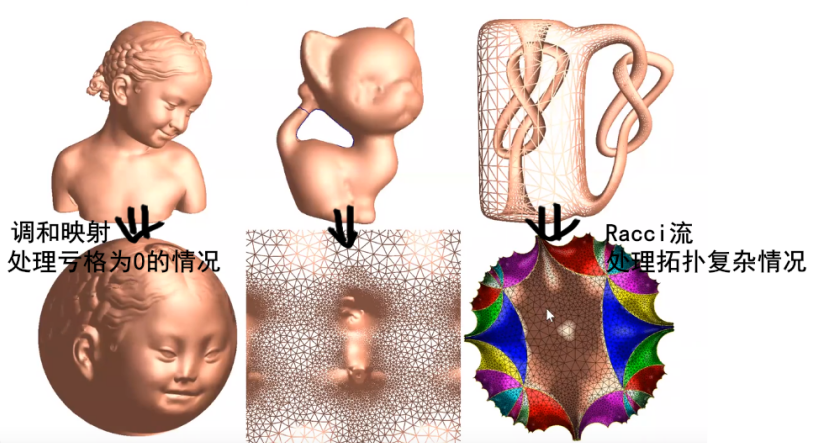
1.调和映射(适用于亏格为0的曲面

2.全纯微分(适用于亏格为1的曲面
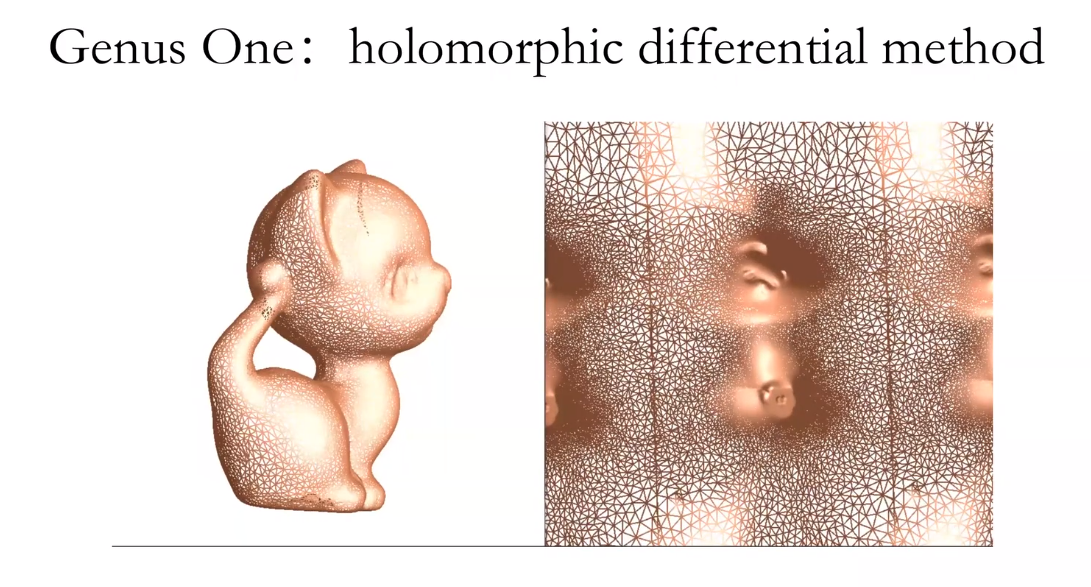
找到散度和梯度为0的像静电场形式的,其映射具有唯一性。
3.Ricci 流(适用于高亏格曲面)
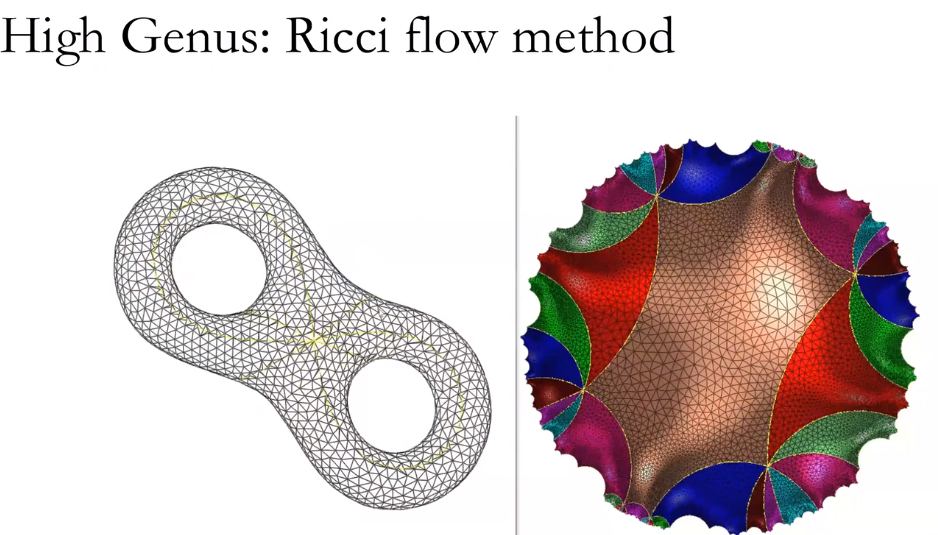
表面纹理映射参数化

传统纹理工艺浪费大量的内存
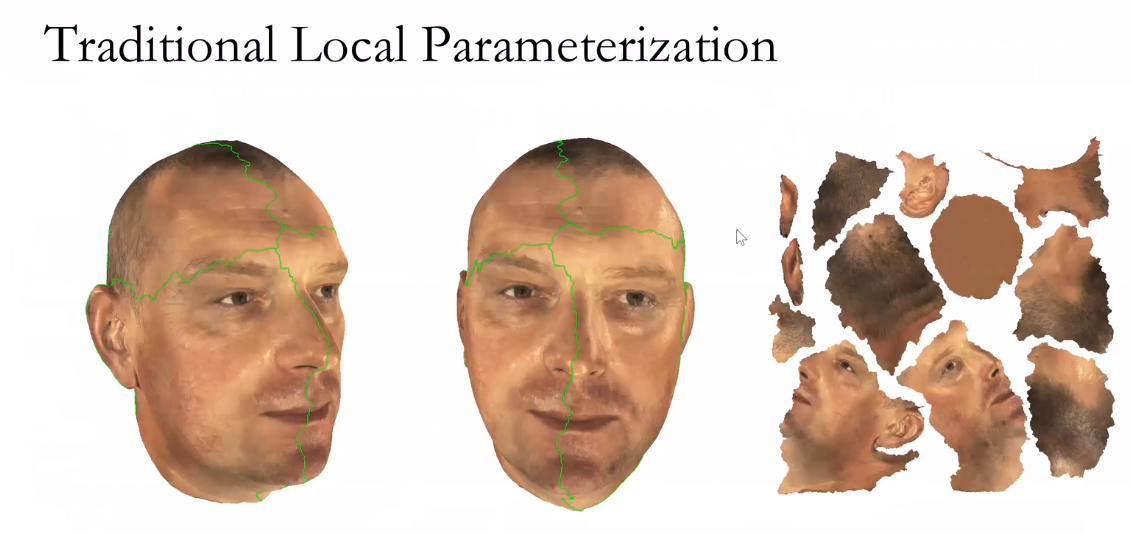
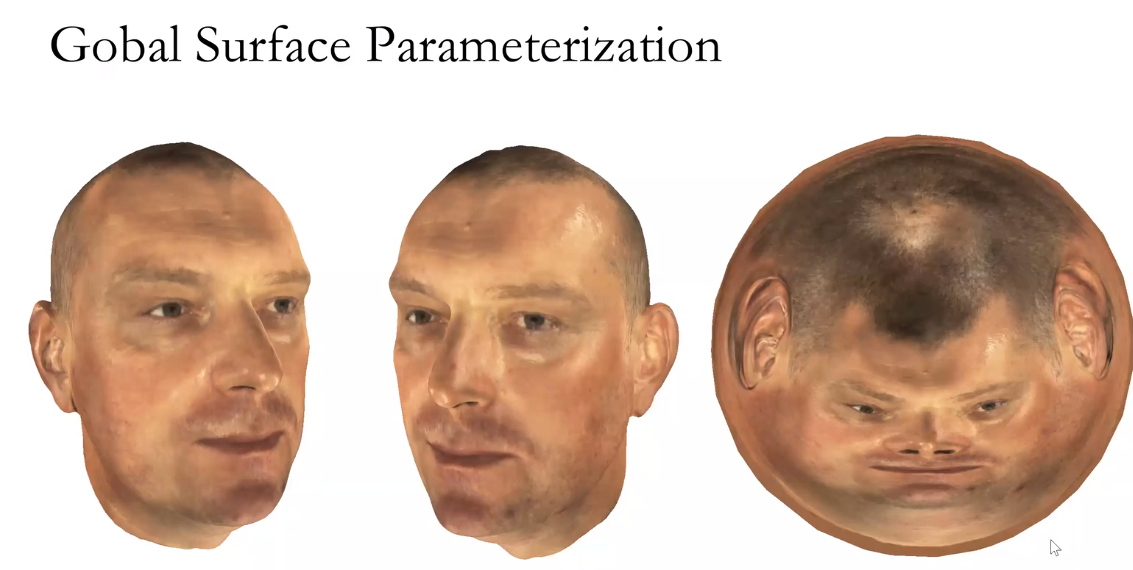
法向映射

保持角度和保持面积的到不同的映射

几何图像
使用2维图像保存3维模型数据。

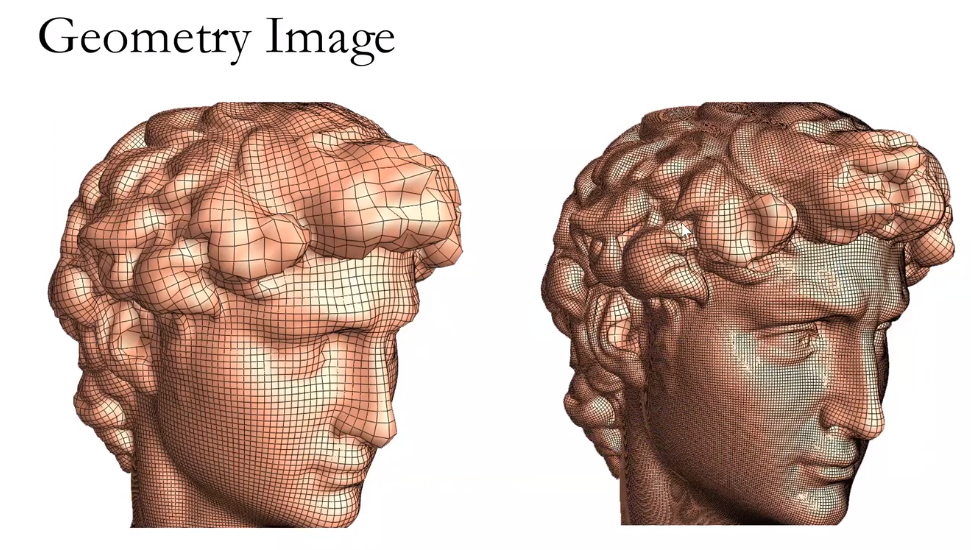

如何处理大量的三维数据
使用三维技术,人们可以非常容易地得到三维的数据结构。
例如使用结构光的方法进行扫描,扫描速度非常快,解析度也高。

动态的表情变化每一帧有差不多50万个采样点。这样可以得到非常迅速的、大规模的三维数据的采集。


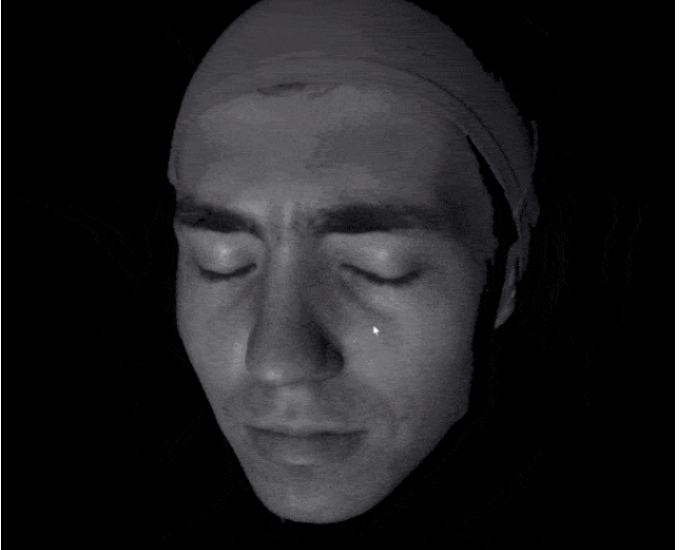
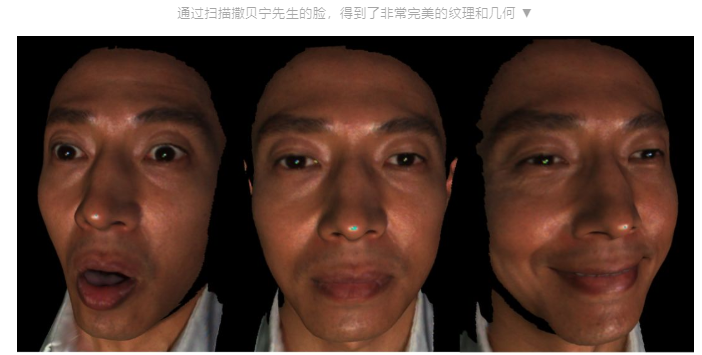
我们瞬间可以得到大量的三维数据,但是如何来处理这些非常难以处理的三维的数据?
平直空间的问题可以使用线性代数,而对于曲面的话无能为力,因此必须要引入现代的微分几何和共形几何。

角度不变,尺寸发生改变。
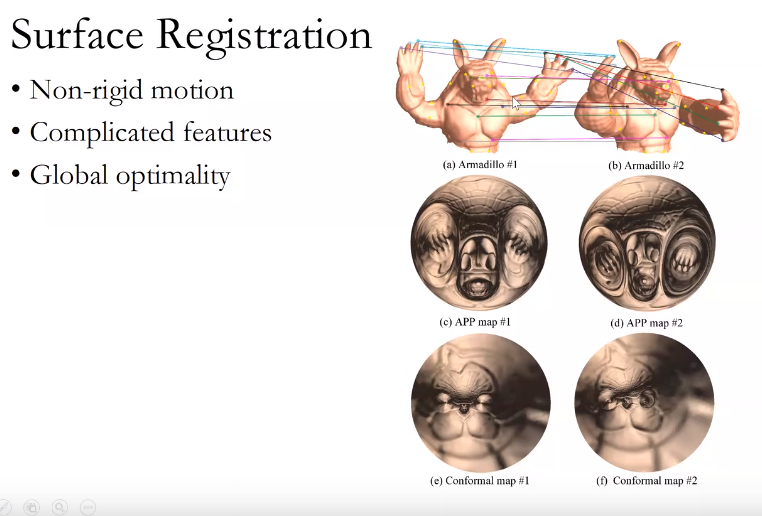
共形几何应用
人脸曲面配准
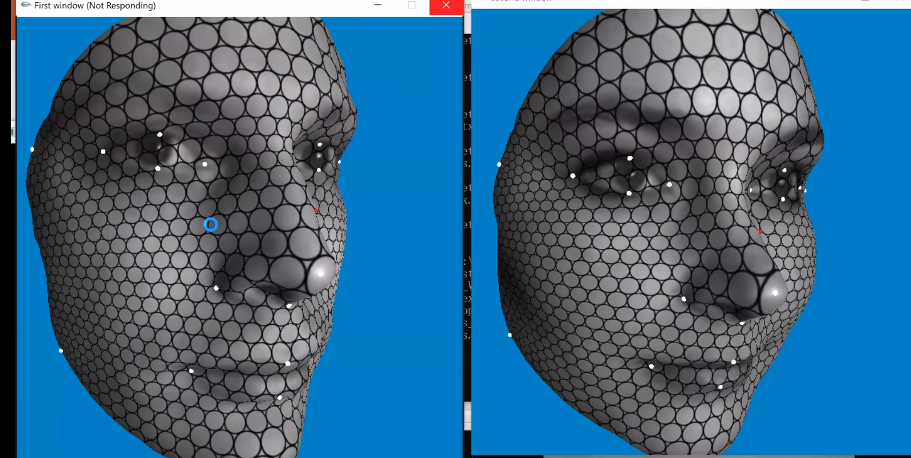
给定两张三维人脸,如何在他们之间,建立比较好的一一映射?我们的方法就是把三维人脸,用黎曼映照,映到二维的圆盘上。这样通过降维攻击,就把这三维问题变成了二维问题。二维问题,会简化非常多。

把这个男孩的这张脸映到女孩这张脸。第一步,用一些机器学习的方法,找到人脸上的特征点,比如眼角、鼻窝还有鼻尖,然后使特征点对齐。第二步,使得整个的畸变达到最小。使畸变最小这个映射,被称为泰希米勒映射。(?

畸变由什么决定呢?是由两族Foliation(叶状结构)决定,调和叶状结构决定。(?
为什么要得到非常精细的映射呢?主要是为了做精准医疗。欧美的白人他们祖先生活在寒带,所以他的基因中缺乏抵御紫外线的功能。所以对于白人来讲,非常容易得皮肤癌,也就是所谓的黑色素瘤。黑色素瘤非常小,肉眼几乎不可见,低于毫米。如果用人工去筛查这个黑色素瘤就会非常痛苦。我们就发明这种方法,同一个人每隔一年扫描一次,然后精细地筛查在皮肤上逐点比较看哪一点皮肤发生突变。这样可以非常自动地找到这个黑色素瘤。所以计算机视觉在医学上也有很深的应用。
三维映射
动画与电影
动作捕捉和表情捕捉
动漫领域,这些方法也有很好的应用。在动漫电影中,动作捕捉和表情捕捉是非常关键的技术。比如武打片的动作捕捉,就是要得到各个关节的信息。但是动作捕捉非常容易,因为人的关节只有几十个,表情捕捉却非常难,表情的自由度有无穷多个。所以现在整个动漫产业,最困难的就是表情捕捉。那么怎么进行表情捕捉呢?
把动态的三维人脸,通过黎曼映照映到二维的圆盘上,然后用刚才的方法可以建立帧与帧之间的一一映射。

哦。也就是说在工程上这些数据的数据量压缩到最小同时保留了角度信息,可以还原。
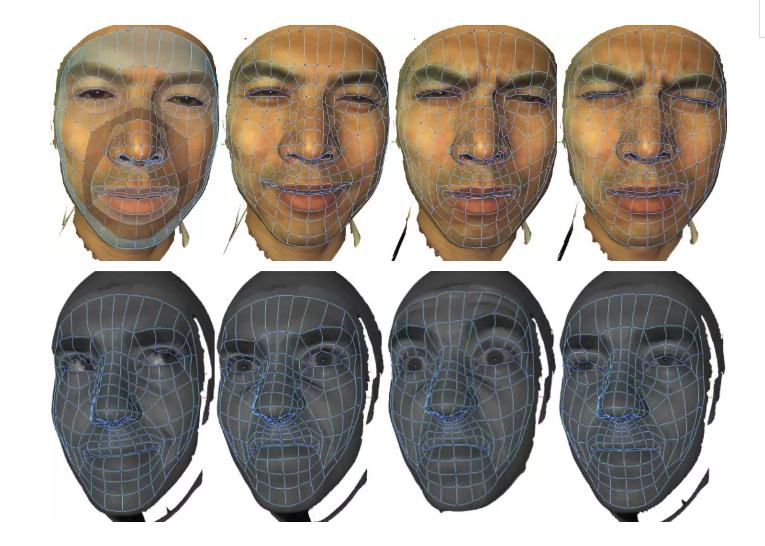
表情移植到卡通人物上
把一张蓝色的四边形网格贴到第一张脸上,依随这个人脸的变化而变化。这个蓝色网格上每一个点会得到三维空间中的一条轨迹,这个轨迹就代表了这个表情的信息。我们可以把这表情信息拿出来,去移植到其他的卡通人物身上。
虚拟演员
把三维的人脸表情拿下来,然后进行表情捕捉。建立一个虚拟演员。

现在明星拍摄非常非常昂贵。那么我们是不是可以把他的所有的表情以三维的方式记录下来,然后导演来决定,到哪一个情节、哪一个台词,用什么表情,从数据库中给它取出来。如果这样,我们不需要这个演员真正来出演,只需要得到他的数字版权就可以。
在这边找了一个演员,把他的一些标准表情给数字化,然后做了下面一个非常小的一个电影片段。这边的整个场景是假的,是用Maya(三维动画)做的。人也是假的,表情也是假的。所以我们相信虚拟演员这个技术,未来可以在VR、AR中很大地普及。

数据压缩
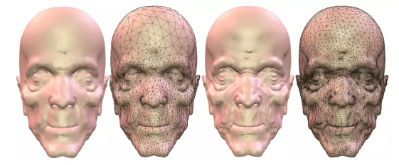
在VR,AR中,数据压缩是一个非常关键的问题。比如我们为了表达一张老人的脸,饱经沧桑、满布皱纹,需要大量的几何信息。如果要通过无线网络来传递这个信息,或者是本身硬件性能比较差,渲染速度就非常慢。如何来压缩这个复杂的几何信息是一个非常关键的问题。我们把一个老人头映到平面的圆盘,然后再控制每个区域在平面上的大小。比如说它曲率比较高的地方,皱纹比较高的地方,让它在平面的区域变得比较大。
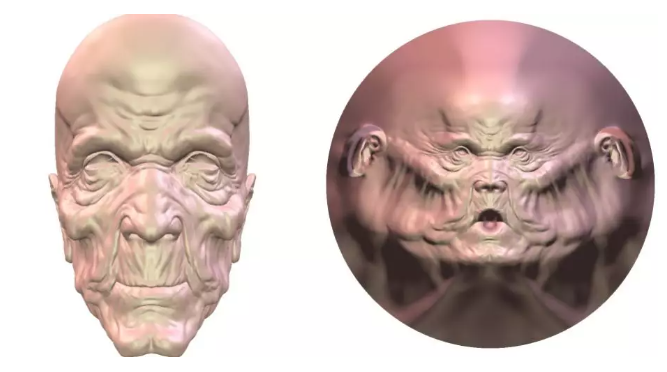
比如这幅图,我们在平面上采样,采样之后在平面上重新进行三角剖分得到这个简化的模型。这边如果我们只用2000个这个采样点,得到的是左侧这张人脸。如果用4000的话得到右侧这张人脸。所以增加采样率,可以使得图像几何的特征越来越细腻。这样就可以求得一个渲染的质量和这个所谓的空间的存储一个很好的一个平衡。这是在VR、AR中几何压缩的一个应用。
医学图像领域
脑图
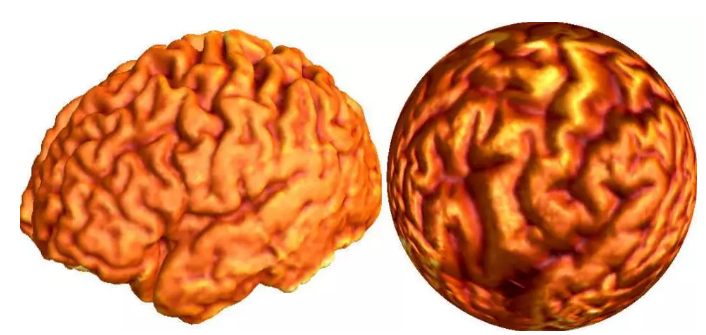
在医学图像领域,共形几何用得也非常广泛,比如说共形脑图。人的大脑,形状非常地复杂,有很多沟回,这些沟回,随着岁月的增长是会发生变化的。比较两个大脑本身来讲非常困难。通过刚才大一统定理,我们知道存在一个共形变换。把大脑映到单位球面上,并且这个映射,基本是唯一的。得到这个映射之后,我们为大脑的每一点,确定唯一的经纬坐标。这样可以在大脑上精确地定位,进行比较。
老年痴呆
老年痴呆症是一个非常普遍的一个疾病。人的大脑根据功能有很多种分区。比如最中间的这个山谷,是胚胎期最先形成的一个皱褶,人的感情,基本存在这个皱褶两边。

下图中,不同颜色代表不同的功能区域。有的区域主管语言,有的区域主管着运动,有的区域主管感情,有的区域主管推理。老年痴呆,是对应的某些功能区域会发生萎缩。
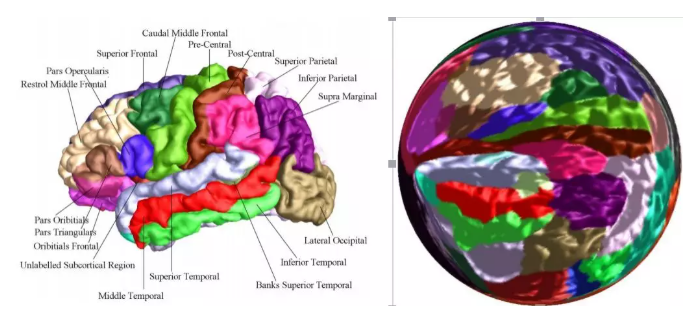
如果我们通过共形脑图,来进行精确的比较,发现老人的语言中枢开始萎缩,可以让他学一门新的外语,这样就可以延缓他老年痴呆症状。如果他的感情中枢开始萎缩,让他多参加社交,如果他的运动中枢开始萎缩,让他去跳广场舞,这样可以加强对这个区域刺激。
癌症检测与虚拟肠镜
在医学图像中的,另外的应用,是关于癌症检测。直肠癌,是男子的第四号杀手,普通男子过了中年之后,肠子里面会长出一些息肉。如果息肉的位置长得不对,经常地摩擦溃疡,摩擦溃疡之后复合,复合之后又反复摩擦溃疡,它的DNA复制次数就会非常多,这样就非常容易出错,出错之后就会形成癌变。
从一个息肉变到癌变,一般需要5到8年,如果在这期间,进行了肠镜检查,就可以非常有效地预防和防止。但是传统的肠镜检查非常痛苦,病人需要全身被麻醉,同时肠镜检查的方式具有非常强的侵犯性。并且老年人的肠壁肌肉非常薄弱,很容易产生非常强烈的并发症。
还有一个很大的问题,直肠有很多皱褶,如果我们的息肉长在皱褶里面的话,传统的光学方法是看不到的,所以用传统的检测方式来进行检查会有大概30%的漏检率。
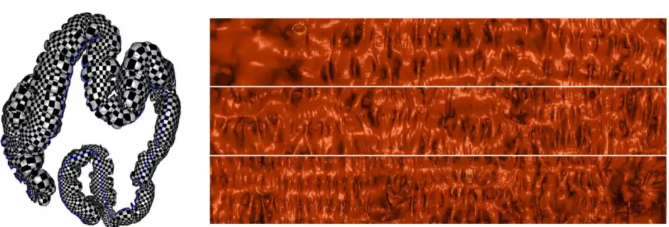
于是我们就发明了虚拟肠镜的方法,核心的想法就是–把肠子的皱褶打开摊平到整个平面上。如果以传统方式来检查,在活人身上是不可能实现的,但是用数字模型可以做到这一点。虚拟肠镜可以把所有肠壁的皱褶给摊开,把所有的息肉暴露出来,然后我们用CT来扫描人的直肠得到数字模型。于是,医生就可以戴上VR眼镜,来观察肠道的内壁。
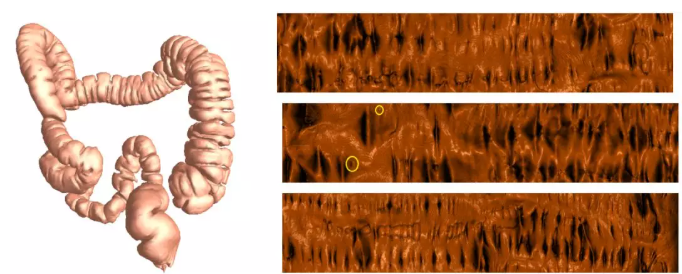
用伪彩色表达肠道内壁,那核心的话我们是要寻找一些肿瘤,或者一些比较大的息肉,那么在这个肠道中探索这个和真实的光学肠镜这个体验是非常相近的。通过这种方法我们就能看到一些比较可疑的息肉。

虚拟肠镜有非常多好处。第一,病人不需要全身麻醉。第二,医生和病人没有肢体接触,第三,我们能暴露所有潜在的息肉,提高诊断的准确率。
这个技术现在北美和日本用得非常普遍,在中国大陆,所有的医院几乎都有这套算法但是很可惜没有被真正用起来。那么它后边基于的是什么?非常艰深的几何用于医疗挽救了非常多的生命。
物联网路由器

交付保证贪婪路由,
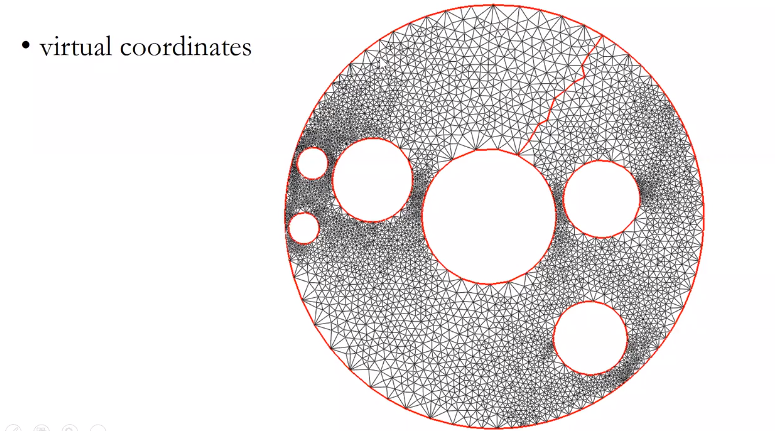
给传感器分配虚拟坐标
整形图像分析

比较微整容前后的差异
工业界
样条曲面要求2阶可导

四边形网格曲面

模拟仿真需要计算高质量的四边形网格,如何生成高质量的网格。


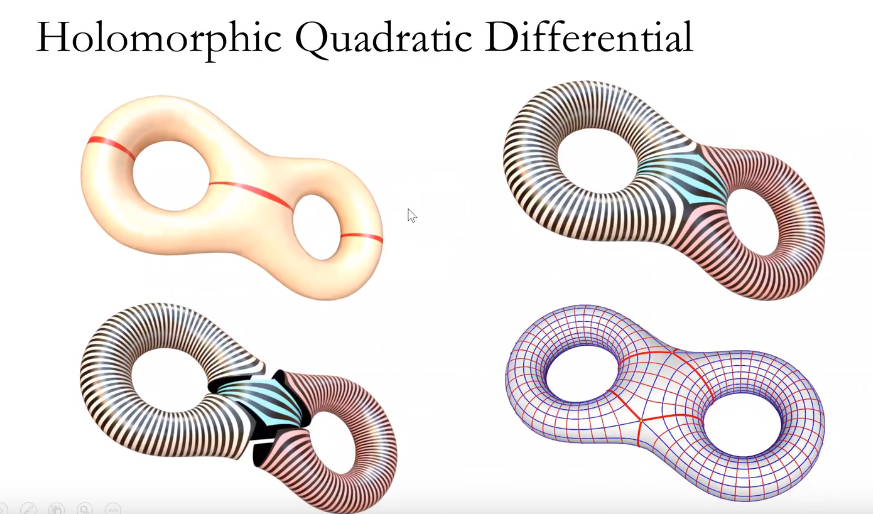

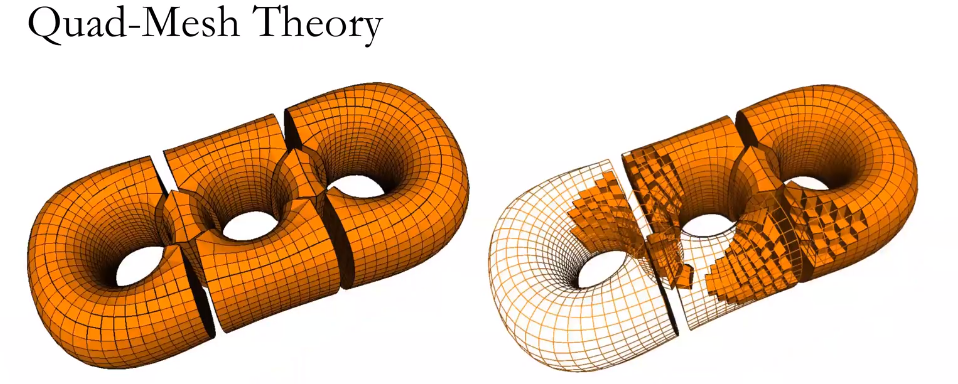



雕塑与力学结构


Reference:
几何为万物赋能——建筑、医疗、动漫、游戏…… | 凤凰卫视世纪大讲堂
Lecture 0 - Introduction to Computational Conformal Geometry